Формулы и свойства треугольников

Содержание статьи

1. Определение треугольника
2. Типы треугольников
3. Свойства треугольников
4. Медианы треугольника
5. Биссектриссы треугольника
6. Высоты треугольника
7. Окружность вписанная в треугольник
8. Окружность описанная вокруг треугольника
9. Взаимосвязь между вписанной и описанной окружностями
10. Средняя линия треугольника
11. Периметр треугольника
12. Формулы площади треугольника
13. Равенство треугольников
14. Подобие треугольников

 

1. Определение треугольника

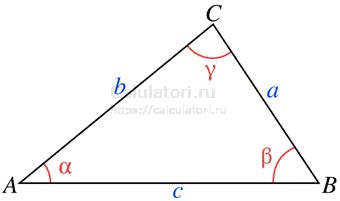
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Тема треугольника является одной из самых увлекательных и интересных в геометрии. Данная геометрическая фигура обладает уникальными свойствами и играет важную роль в различных областях и науках.

Треугольники подразделяются по различным признакам, таким как длина сторон – равносторонний, равнобедренный или разносторонний. А также по величине  углов: остроугольный, тупоугольный или прямоугольный.

Сумма углов треугольника всегда будет равна 180 градусам. Этот факт лежит в основе теоремы о сумме углов треугольника, которая является основой многих математических рассуждений. Треугольники применяются в различных областях жизни, таких как архитектура и  дизайн, а также физика и инженерия. На их основе проектируются и строятся различные конструкции и формы, а также их используют при расчете и моделировании.

Изучение этих геометрических фигур позволяет развить логическое мышление и математические навыки. Таким образом изучение этой фигуры является неотъемлемым элементом в образовании и позволяет понять мир вокруг нас более глубоко.

2. Виды треугольников

Треугольники бывают разных видов и классифицируются в зависимости от своих сторон и углов. Давайте рассмотрим основные виды треугольников.

По количеству равных сторон или степени симметрии треугольники подразделяются на следующие виды:

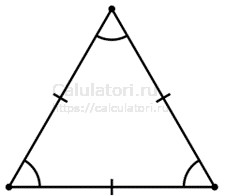
1. Равносторонний треугольник - это треугольник, в котором все три стороны и углы при основании равны. Такие треугольники являются высоко симметричными фигурами. На их основе строятся многие другие фигуры.
   
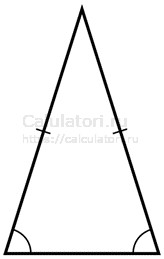
2. Равнобедренный треугольник - это треугольник, в котором две стороны имеют равную длину. Эти равные стороны называются боковыми, а третья сторона — основанием. В таком треугольнике углы при основании равны. Также в равнобедренном треугольнике равны две медианы, две высоты, две биссектрисы.
   
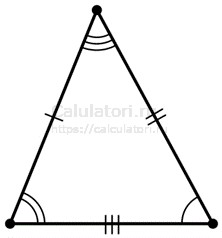
3. Разносторонний треугольник: это треугольник, у которого все стороны различны. В таких треугольниках углы также могут быть разными, что делает их наиболее разнообразными среди всех видов треугольников.
   

В свою очередь по виду наибольшего угла треугольники подразделяются на:

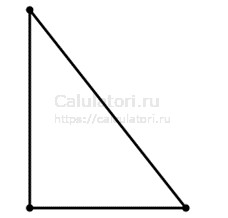
1. Прямоугольный треугольник: в таком треугольнике один из углов равен 90 градусам. Прямоугольные треугольники широко используются в различных научных и инженерных расчетах, а также в повседневной жизни для измерения расстояний и построения перпендикуляров.
   
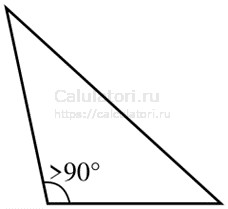
2. Тупоугольный треугольник: в таком треугольнике наибольший угол больше 90 градусов. Два остальных угла являются острыми.
   
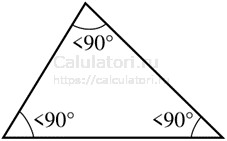
3. Остроугольный треугольник: в таком треугольнике все углы являются острыми.
   

Итак, треугольники – это удивительные геометрические фигуры, способные поражать своим разнообразием и красотой. Каждый вид треугольника имеет свои уникальные свойства и применения, делая изучение этой фигуры увлекательным и интересным занятием.

3. Свойства треугольников

Треугольник – одна из основных фигур в геометрии, и изучение его свойств является важной частью математического образования. Давайте рассмотрим некоторые основные свойства треугольников. 

 

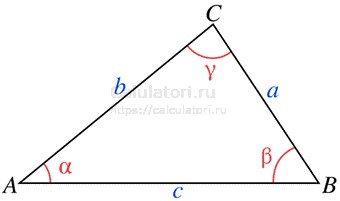
• Сумма углов треугольника всегда равна 180 градусам. Это называется теоремой о сумме углов в треугольнике. Независимо от формы или размера треугольника, сумма всех его углов всегда будет равна 180 градусам.

  $\alpha +\beta +\gamma =180°$

• Неравенство треугольника. Сумма длин двух сторон треугольника всегда больше длины третьей стороны. Это свойство называется неравенством треугольника и является одним из основополагающих принципов геометрии.

  $A<B+C; B<A+C; C<A+B$

• Сравнение сторон и углов. Напротив большего угла треугольника всегда лежит большая его сторона.
• Внешний угол. Любой внешний угол треугольника равен сумме двух внутренних углов не смежных с ним.

  

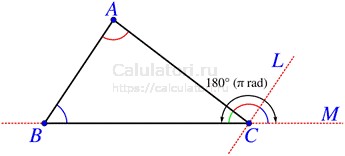
• Теорема синусов. Данная теорема устанавливает связь между длинами сторон и величиной противолежащих им углов.

  $\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R$

  где R – радиус окружности, описанной вокруг треугольника

• Теорема косинусов. Является обобщенной формой теоремы Пифагора.

  $a^2=b^2+c^2-2bc·cos\alpha$

Знание этих и других свойств треугольников позволяет решать различные задачи в математике, строить графику, а также находить практические применения в повседневной жизни. Геометрия – это увлекательная и важная область математики, которая помогает нам лучше понимать окружающий мир.

4. Медианы треугольника

Медиана — одна из важнейших линий в геометрии треугольников. Это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Каждая вершина имеет свою медиану, следовательно, у любого треугольника ровно три медианы.

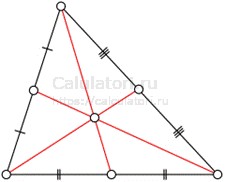
• Разделение площади пополам. Медиана разделяет треугольник на два равных по площади треугольника. Если провести медиану из вершины A в сторону BC, то площадь каждого образовавшегося треугольника ΔABM и ΔACM, где M — середина BC, равна половине площади исходного треугольника ABC.

  $S_{{}_{\Delta }ABM}=S_{{}_{\Delta }ACM}=\frac{S_{{}_{\Delta }ABC}}{2}$

• Пересечение всех трех медиан в одной точке. Все три медианы пересекаются в одной точке, называемой центром тяжести (или центроидом) треугольника. Эта точка расположена на расстоянии двух третей длины каждой медианы от соответствующей вершины и одной трети расстояния от противоположной стороны.

   

• Длина медианы связана с длинами сторон треугольника. Существует формула для вычисления длины медианы, исходя из длин сторон треугольника:

  $m_a=\sqrt{\frac{2b^2+2c^2-a^2}{4}}$

  где a, b и c— длины сторон треугольника, а — длина медианы, проведенной к стороне a.

Таким образом, медианы играют ключевую роль в изучении свойств геометрических фигур и широко используются в различных областях математики и физики.

5. Биссектрисы треугольника

Биссектриса — это линия, делящая угол треугольника на две равные части. Точка пересечения биссектрисы с противоположной стороной называется точкой деления стороны. Каждый угол треугольника имеет свою собственную биссектрису, соответственно, у любого треугольника существует ровно три биссектрисы.

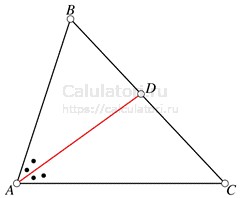
Основные свойства биссектрисы: 

• Свойства точки пересечения. Все три биссектрисы треугольника пересекаются в одной точке, называемой инцентром. Инцентр — центр вписанной окружности, касающейся всех трёх сторон треугольника.
• Теорема о пропорциональности. Биссектриса делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам. То есть, если биссектриса проведена из вершины А к стороне ВС, то отношение частей, на которые делится сторона, равно отношению прилежащих сторон АВ и АС:

  $\frac{BD}{DC}=\frac{AB}{AC}$

• Формула длины биссектрисы. Длина биссектрисы может быть найдена по формуле, связанной с длинами сторон треугольника. Для биссектрисы, проведённой из вершины A к стороне BC, её длина определяется следующим образом:

  $L_a=\frac{2·AB·AC}{AB+AC}\cos \left(\frac{BC}{2}\right)$

Таким образом, изучение свойств биссектрис помогает глубже понять симметрию и пропорции внутри треугольника, делая этот элемент важным инструментом как в теоретической математике, так и в прикладных дисциплинах.

6. Высоты треугольника

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую ей сторону (или продолжение этой стороны). У каждого треугольника имеется ровно три высоты, поскольку каждую вершину можно соединить с противоположной стороной посредством перпендикуляра (то есть образующая с ней угол 90 градусов).

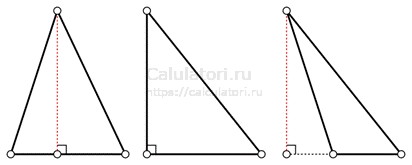
• Пересечение высот. Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла. Ортоцентр изогонально сопряжен центру описанной окружности. Ортоцентр лежит на одной прямой с центроидом и центром описанной окружности.

  

• Если в треугольнике две высоты равны, то треугольник — равнобедренный, и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит. Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
• Зависимость между высотой и площадью. Площадь треугольника напрямую связана с длиной его высоты. Формула площади через высоту выглядит следующим образом:

  $S=\frac{1}{2}ah$

  где a – основание треугольника, а h – проведенная к этому основанию высота.

• Связь с радиусом описанной окружности. Радиус описанной окружности (R) и высота связаны формулой Эйлера:

  $OH=|R^2-h^2|$

  где H – ортоцентр, О – центр описанной окружности, h – высота.

  Также соблюдается следующая зависимость:

  $\left|OH\right|=\sqrt{9R^2-(a^2+b^2+c^2)}$

  где a, b и c – длины сторон треугольника.

Эти свойства делают высоты важнейшим элементом исследования свойств треугольников, позволяя решать различные задачи и применять знания в разных сферах науки и техники.

7. Окружность вписанная в треугольник

Окружностью, вписанной в треугольник, называют такую окружность, которая касается всех трех сторон фигуры изнутри. Центр этой окружности лежит на пересечении биссектрис углов треугольника и носит название инцентра.

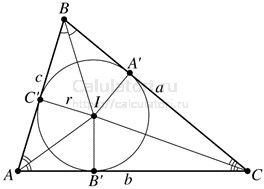
Свойства вписанной окружности:

• Расстояние от инцентра до сторон постоянно. Из-за особенностей расположения центра и условий касания расстояние от центра вписанной окружности до каждой стороны треугольника одинаково и представляет собой радиус окружности (r). Таким образом, любая прямая, проведённая из центра перпендикулярно какой-либо стороне, даст длину радиуса.
• Площадь и радиус взаимосвязаны. Можно выразить площадь треугольника через радиус вписанной окружности и полупериметр:

  $S=pr$

  где S— площадь треугольника, p — полупериметр, r — радиус вписанной окружности.

  Эта связь делает удобным использование радиуса вписанной окружности при расчетах площадей и решении задач, связанных с периметрами.
• Формулы нахождения радиуса. Существуют разные способы расчета радиуса вписанной окружности:
  -Через площадь и полупериметр:

  $r=\frac{S}{p}$

  - По известным сторонам треугольника (формула Герона):

  $r=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}$

  где a, b и c - длины сторон треугольника

Вписанные окружности важны не только в классической евклидовой геометрии, но и находят применение в теории функций, механике, архитектуре и инженерии. Знание свойств вписанных окружностей облегчает решение многих практических задач, особенно связанных с расчетами площадей, оптимизацией конструкций и распределением нагрузок.

8. Окружность описанная вокруг треугольника

Описанной окружностью треугольника называется такая окружность, которая проходит через три вершины треугольника. Центр описанной окружности лежит на пересечении серединных перпендикуляров сторон треугольника. Серединный перпендикуляр — это прямая, проходящая через середину стороны и перпендикулярно ей.

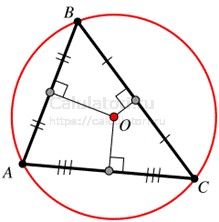
Свойства описанной окружности:

• Радиус описанной окружности обозначается буквой R. Его можно вычислить различными способами, наиболее распространенными являются следующие формулы:

  $R=\frac{AB}{2 \sin C}; R=\frac{BC}{2 \sin A}; R=\frac{AC}{2 \sin B};$

  где AB, BC и AC – длины сторон треугольник, а А, B и C - величины противолежащих им углов.

• Площадь треугольника связана с радиусом описанной окружности следующим образом:

  $S=\frac{AB·BC·CA}{4R}$

• Точки пересечения высот треугольника образуют ортотреугольник, описанная окружность которого совпадает с описанной окружностью исходного треугольника.
• Центры вписанной и описанной окружностей в равностороннем треугольнике совпадают.

9. Взаимосвязь между вписанной и описанной окружностями треугольника

Ранее были рассмотрены две важные для треугольника окружности: вписанная и описанная. Они обладают рядом уникальных свойств и закономерностей, связывающих их друг с другом.

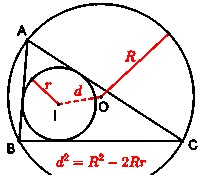
Основные связи и соотношения:

1.Общее расположение центров. Центры обеих окружностей расположены внутри треугольника, однако их положения различны:

• Центр описанной окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника.
• Центр вписанной окружности совпадает с точкой пересечения биссектрис внутренних углов треугольника.

2. Отношения радиусов. Обозначим радиусы следующим образом: 

• r - радиус вписанной окружности.
• R - радиус описанной окружности.

Между этими величинами существует известная зависимость:

$R\ge r$

Это неравенство показывает, что радиус описанной окружности всегда больше либо равен радиусу вписанной окружности.

3. Формула Эйлера. Расстояние между центрами вписанной и описанной окружностей обозначается буквой d. Оно связано с радиусами следующей формулой:

$d^2=R(R-2r)$

Эта формула известна как теорема Эйлера. Она полезна для расчёта расстояний между центрами окружностей и проверки гипотез относительно конкретных значений радиусов.

4. Рассмотрим некоторые частные случаи:

• Равносторонний треугольник. Здесь центры обеих окружностей совпадают, и соотношение радиусов становится простым:

  $R=2r$

• Прямоугольный треугольник. Особенность прямоугольного треугольника заключается в том, что центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.

10. Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Важнейшая особенность средней линии состоит в том, что она параллельна третьей стороне и равна её половине.

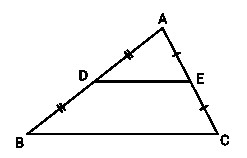
Основные свойства средней линии:

• Параллельность и пропорциональность. Средняя линия параллельна третьей стороне треугольника и вдвое короче неё. Другими словами, если отрезок DE — средняя линия, проведённая между сторонами AB и AC, то DE || BC и $DE=\frac{BC}{2}$.
• Делит треугольник на подобную фигуру. Проведение средней линии образует меньший треугольник, ограниченный ею. При этом он подобен исходному треугольнику с коэффициентом подобия равным $\frac{1}{2}$. Проведя все средние линии треугольника, мы формируем четыре малых треугольника, каждый из которых подобен исходному треугольнику с коэффициентом подобия $\frac{1}{2}$ .
• Проводя средние линии треугольника попарно, мы формируем четырёхугольник, который является параллелограммом.
• Центральная точка. Пересечение средних линий проходит через центр тяжести треугольника (точку пересечения медиан).

Эти свойства позволяют эффективно использовать среднюю линию в задачах по определению пропорций, похожести треугольников и проверке коллинеарности точек.

11. Периметр треугольника

Периметр треугольника — это сумма длин всех его сторон. Данный показатель важен в геометрии и применяется в различных задачах, включая расчеты площади, исследование подобия и сравнение фигур.

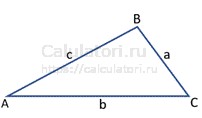
Как рассчитать периметр треугольника?

Чтобы найти периметр треугольника, достаточно сложить длины всех трех его сторон. Если известны длины сторон a, b и c, то периметр (P) рассчитывается по простой формуле:

$P=a+b+c$

Также периметр связан с площадью через радиус вписанной окружности:

$P=\frac{2S}{r}$

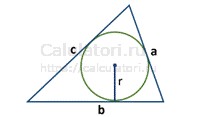
Рассмотрим некоторые частные случаи:

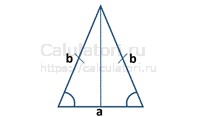
• Равнобедренный треугольник. Это треугольник, в котором две стороны равны. В таком случае формула расчёта периметра примет вид:

  

  $P=a+2b$

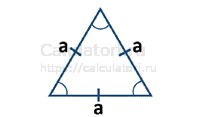
• Равносторонний треугольник. Это треугольник, в котором все стороны равны. Получаем следующую формулу:

  

  $P=3a$

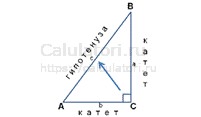
• Прямоугольный треугольник. Это треугольник, в котором один из углов равен 90 градусам. Длины сторон такого треугольника связаны теоремой Пифагора: ${с}^2=a^2+b^2$В таком случае формула расчёта периметра может принимать следующие виды:

  

  $P=a+b+\sqrt{a^2+b^2}$

  $P=b+c+\sqrt{c^2-b^2}$

  $P=a+c+\sqrt{c^2-a^2}$

Полупериметр

Иногда удобно пользоваться понятием полупериметра (p), которое равно половине периметра:

$p=\frac{P}{2}=\frac{a+b+c}{2}$

Полупериметр часто встречается в формулах, связанных с площадями и радиусами вписанных и описанных окружностей.

12. Площадь треугольника

Площадь треугольника — одно из ключевых понятий в геометрии, позволяющее определить размер плоской поверхности, ограниченной тремя сторонами. Знание методов расчета площади важно не только в учебной практике, но и в повседневных ситуациях, таких как ремонт помещений, проектирование ландшафтов и многое другое.

Методы расчета площади треугольника

• Классическая формула Герона
  Используется, если известны длины всех трех сторон треугольника. Формула Герона выражается следующим образом:

  $S=\sqrt{p(p-a)(p-b)(p-c)}$

  где S - искомая площадь, a, b, c - длины сторон треугольника, p - полупериметр

• Использование высоты
  Наиболее простая формула применима, если известна длина одной стороны и высота, проведённая к этой стороне:

  $S=\frac{1}{2}bh$

  где b - длина стороны (основание), h - высота, опущенная на эту сторону.

• Использование двух сторон и угла между ними
  В случае, если известны длины двух сторон и значение угла между ними, для нахождения площади можно воспользоваться следующей формулой:

  $S=\frac{1}{2} ab·\sin \alpha$

  где a и b – известные стороны треугольника, а – угол между ними.

• Использование радиуса описанной окружности
  В случае, если известны длины сторон и радиус описанной окружности, площадь можно найти следующим образом:

  $S=\frac{abc}{R}$

  где a, b и c – стороны треугольника, а R – радиус описанной окружности

• Использование радиуса вписанной окружности
  В случае, если известны длины сторон и радиус вписанной окружности, площадь можно найти следующим образом:

  $S=pr$

  где p – полупериметр, а r – радиус вписанной окружности

• Использование стороны и двух прилежащих углов

  $S=\frac{a^{2}sin\alpha ·sin\beta }{2\sin (\alpha +\beta )}$

13. Подобие треугольников

Подобие треугольников — это важное понятие в геометрии, отражающее сходство формы двух треугольников независимо от размера. Два треугольника называются подобными, если их соответствующие углы равны, а стороны пропорциональны.

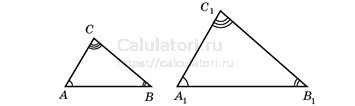
Признаки подобия треугольников

Есть несколько основных признаков, по которым можно установить подобие треугольников:

• По двум углам. Если два угла одного треугольника равны соответствующим углам другого треугольника, то такие треугольники подобны.
• По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между соответствующими сторонами равны, то треугольники подобны.
• По трем сторонам. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Коэффициент подобия

Коэффициент подобия — это число, показывающее степень увеличения или уменьшения размеров одного треугольника относительно другого. Если длины соответствующих сторон треугольников относятся как k, то говорят, что коэффициент подобия равен k. Например, если известно, что сторона одного треугольника составляет половину аналогичной стороны другого, то коэффициент подобия равен 0.5.

Свойства подобных треугольников

• Соответствующие углы равны.

  $A=A_1;B=B_1;C=C_1$

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

  $\frac{S_1}{S}=k^2$

• Соотношение соответствующих линейных величин (например, периметров) также равно коэффициенту подобия.

14. Равенство треугольников

Два треугольника называются равными, если они полностью совпадают при наложении друг на друга, то есть их соответствующие элементы (стороны и углы) абсолютно одинаковы. Иначе говоря, равенство треугольников означает совпадение всех их сторон и углов.

Признаки равенства треугольников

• По двум сторонам и углу между ними. Если две стороны одного треугольника равны двум сторонам другого треугольника, а угол между этими сторонами тоже равен, то такие треугольники равны.

  $b=b_1 и c=c_1 и A=A_1\to △ABC=△A_1{B}_1{C}_1$

• По стороне и двум прилежащим углам. Если сторона одного треугольника равна стороне другого треугольника, а углы, прилежащие к этой стороне, равны, то треугольники равны.

  $a=a_1 и B=B_1 и C=C_1\to △ABC=△A_1{B}_1{C}_1$

• По трем сторонам. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

  $a=a_1 и b=b_1 и c=c_1\to △ABC=△A_1{B}_1{C}_1$

Важно отметить, что при применении указанных признаков порядок сопоставляемых элементов должен соблюдаться строго.

Следствия равенства треугольников

• Стороны, лежащие напротив равных углов, равны.
• Углы, лежащие напротив равных сторон, равны.
• Соответствующие высоты, медианы и биссектрисы также равны.