Трапеция Формулы, признаки и свойства
Содержание
- Определение трапеции
- Элементы трапеции
- Виды трапеций
- Основные свойства трапеции
- Стороны трапеции
- Средняя линия трапеции
- Высота трапеции
- Диагонали трапеции
- Площадь трапеции
- Периметр трапеции
- Окружность описанная вокруг трапеции
- Окружность вписанная в трапецию
Определение трапеции
Трапеция - это четырёхугольник, в котором две стороны параллельны, а две другие не параллельны. Также сущуствует и другой вариант определения.
Трапеция - это четырёхугольник в котором две противоположные стороны параллельны и не равны. Оба определения равнозначны.
Трапеция - это четырёхугольник в котором две противоположные стороны параллельны и не равны. Оба определения равнозначны.
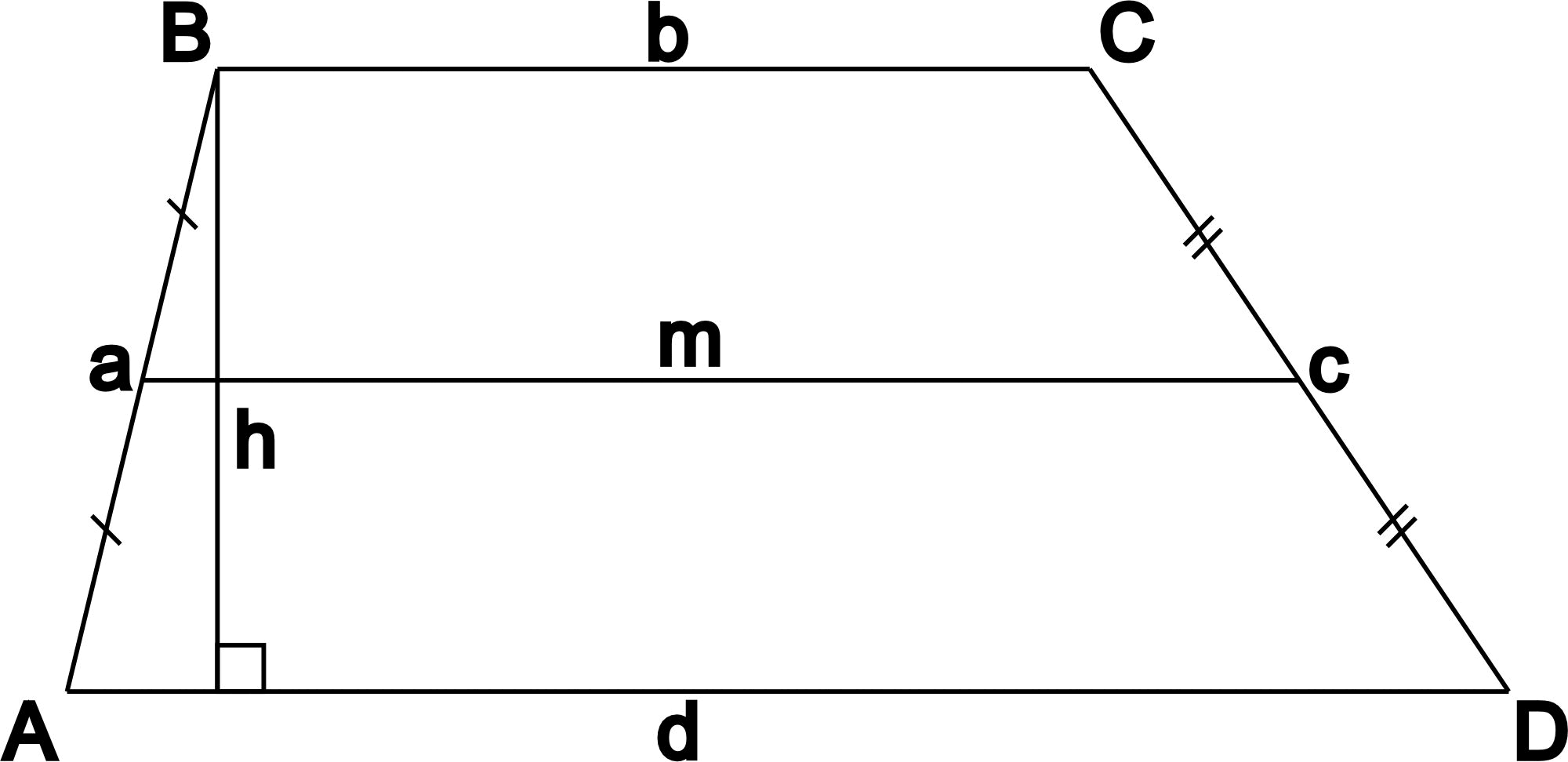
На рисунке a, b, c и d - стороны трапеции, A, B, C и D - углы трапеции, h- высота, m - средняя линия.
Элементы трапеции
Все трапеции обладают следующими элементами:- Основания трапеции - две параллельные противоположные стороны. В нашем случае это стороны b и d.
- Боковые стороны - две непараллельные противоположные стороны. В нашем случае - a и c.
- Средняя линия - отрезок, соединяющий середины боковых сторон. На рисунке обозначен как m.
- Угол при основании - угол, образованный основанием с боковой стороной.
Виды трапеций
Трапеции подразделяются на следующие виды:- Равнобедреннная - трапеция, в которой боковые стороны равны.
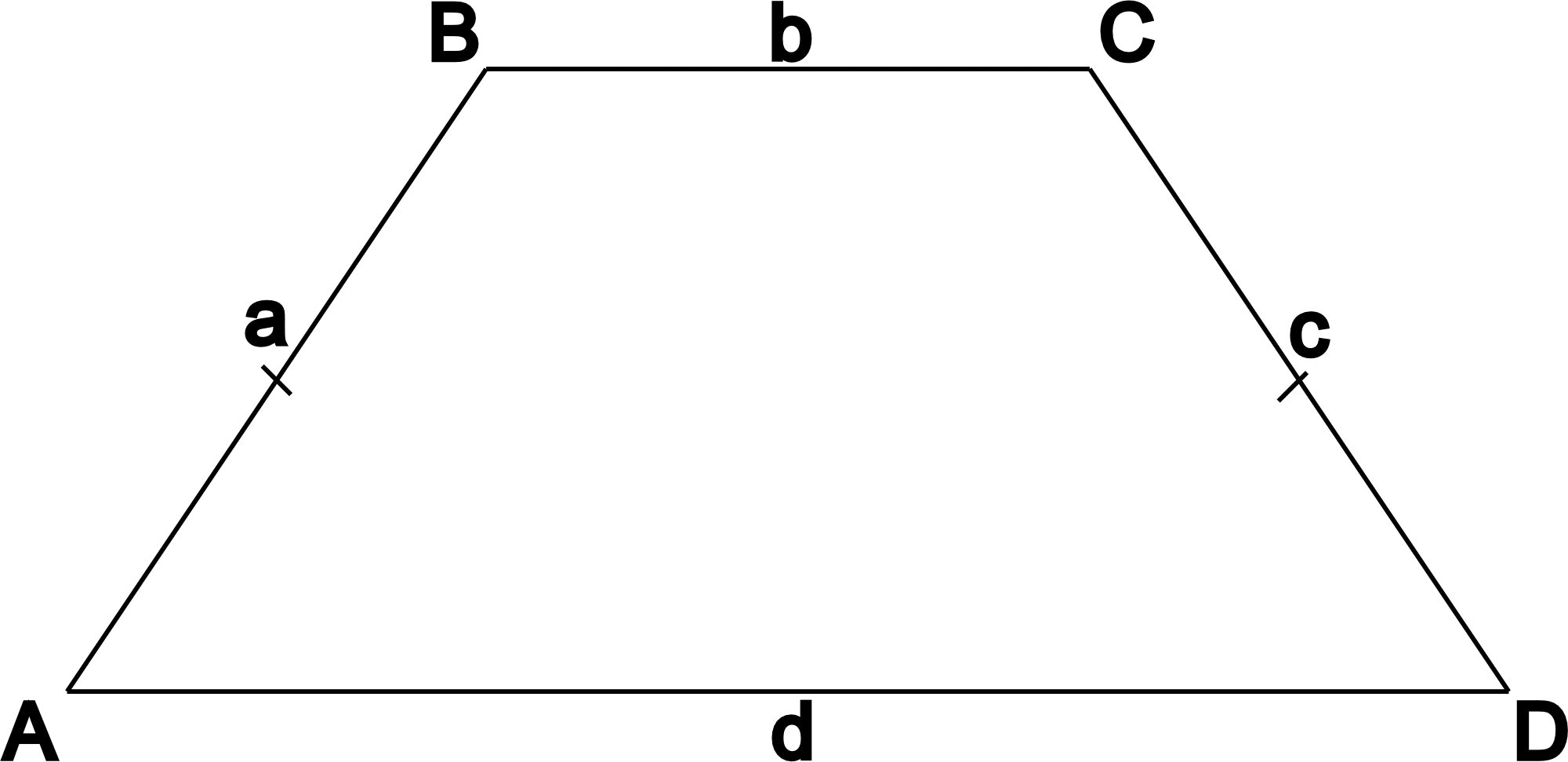
Также существует несколько других признаков равнобедренной трапеции, коротко их упомянем. Трапеция является равнобедренной, если:
- Отрезок, соединяющий середины оснований, перпендикулярен им.
- Углы при любом основании равны
- Сумма противоположных углов равна 180 градусам
- Длины диагоналей равны
- Высота делит большее основание на два отрезка, один из которых равен полусумме оснований, а другой полуразности
- Вокруг этой трапеции можно описать окружность
- Средняя линия равна высоте
- Прямоугольная - трапеция, в которой угол при основании прямой, то есть равен 90 градусов.
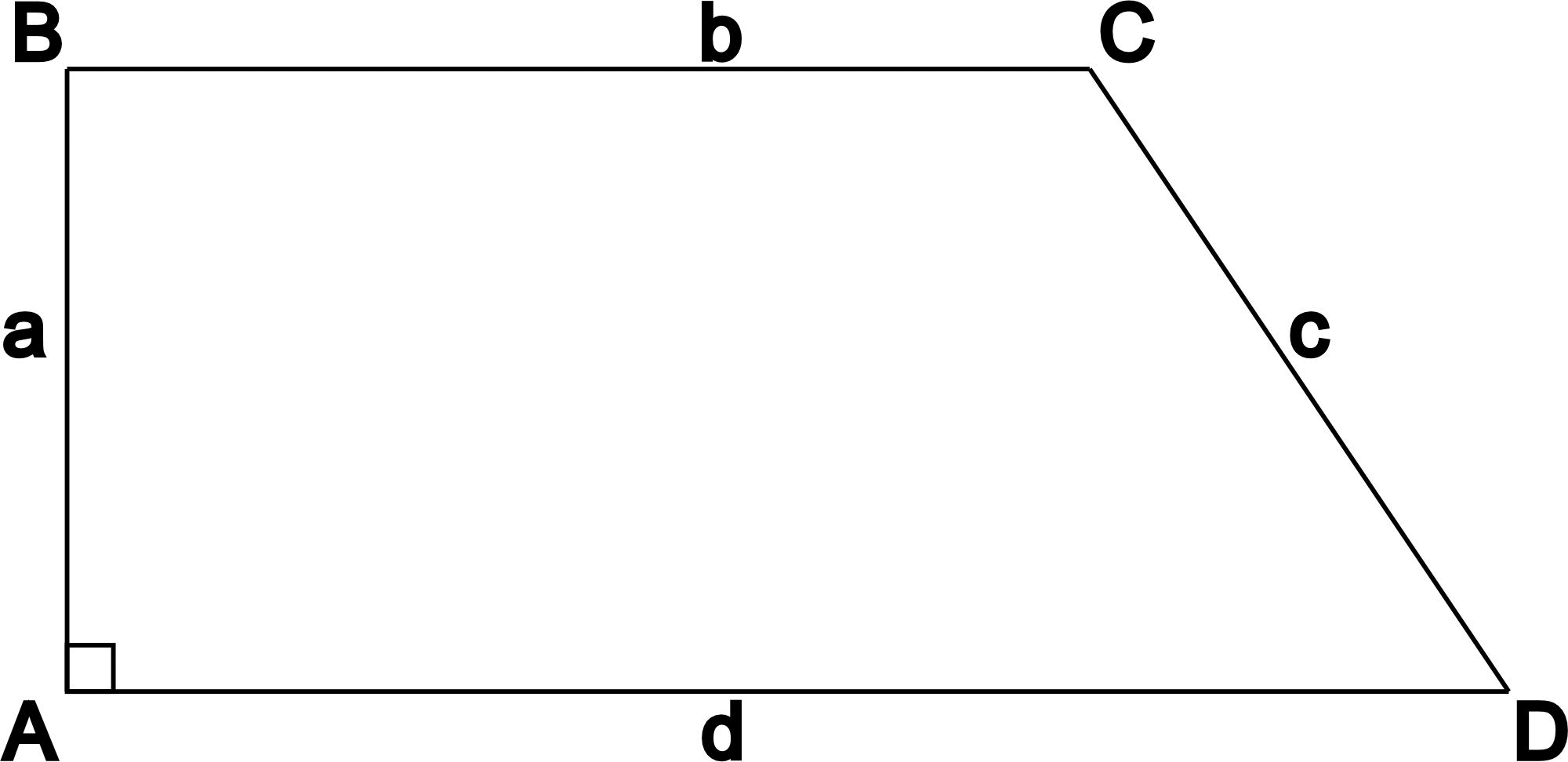
- Произвольная - трапеция, не являющаяся равнобедренной или прямоугольной.
Основные свойства трапеции
Трапеция обладает следующими основными свойствами:- Сумма углов, прилежащих к одной из одной из боковых сторон трапеции равна 180 градусам.
- В трапецию можно вписать окружность, если сумма длин её оснований равна сумме длин боковых сторон.
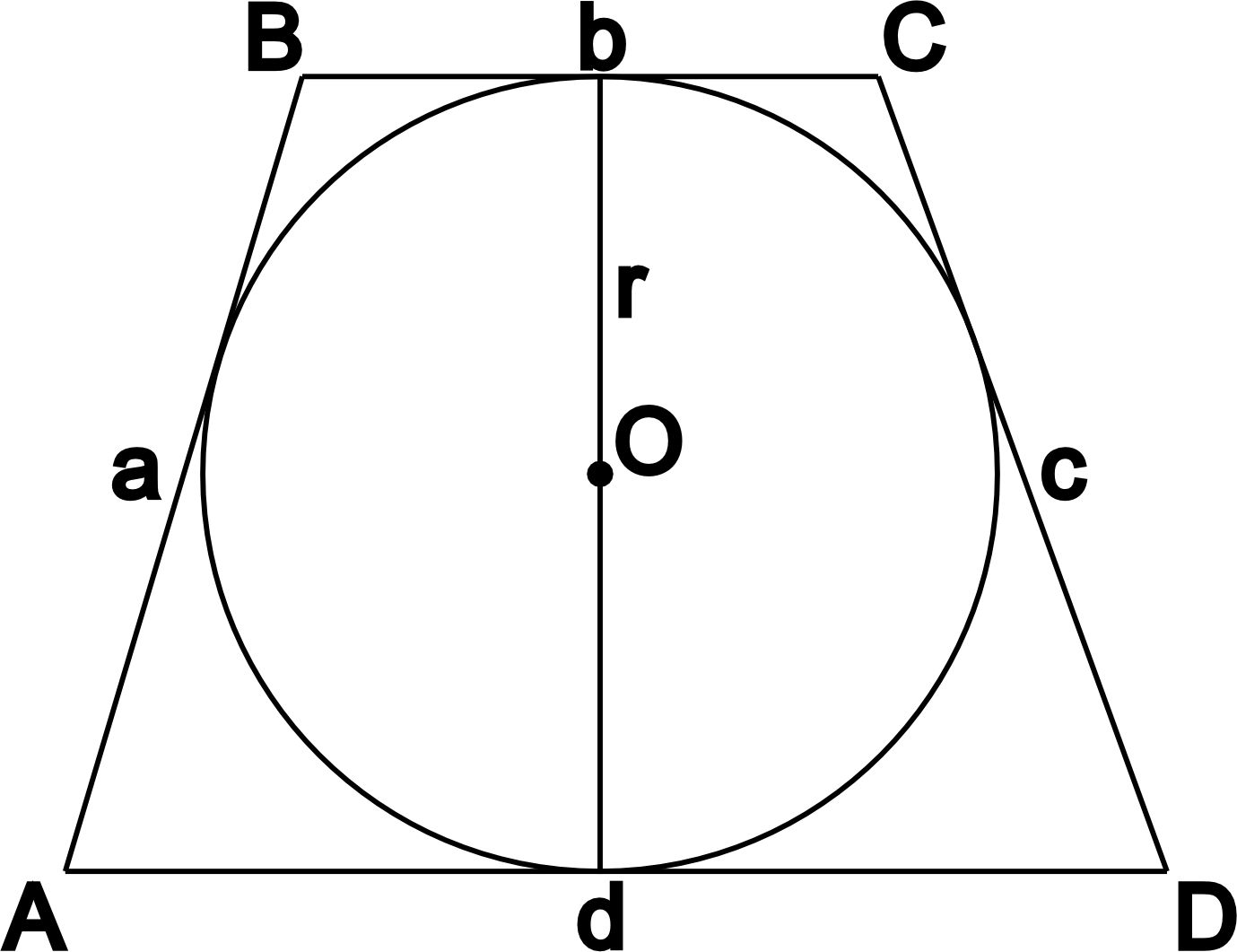
- Боковая сторона видна из центра описанной окружности под углом 90 градусов.
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Средняя линия разделяет пополам любой отрезок, соеднияющий основания, пополам и также делит пополам диагонали.
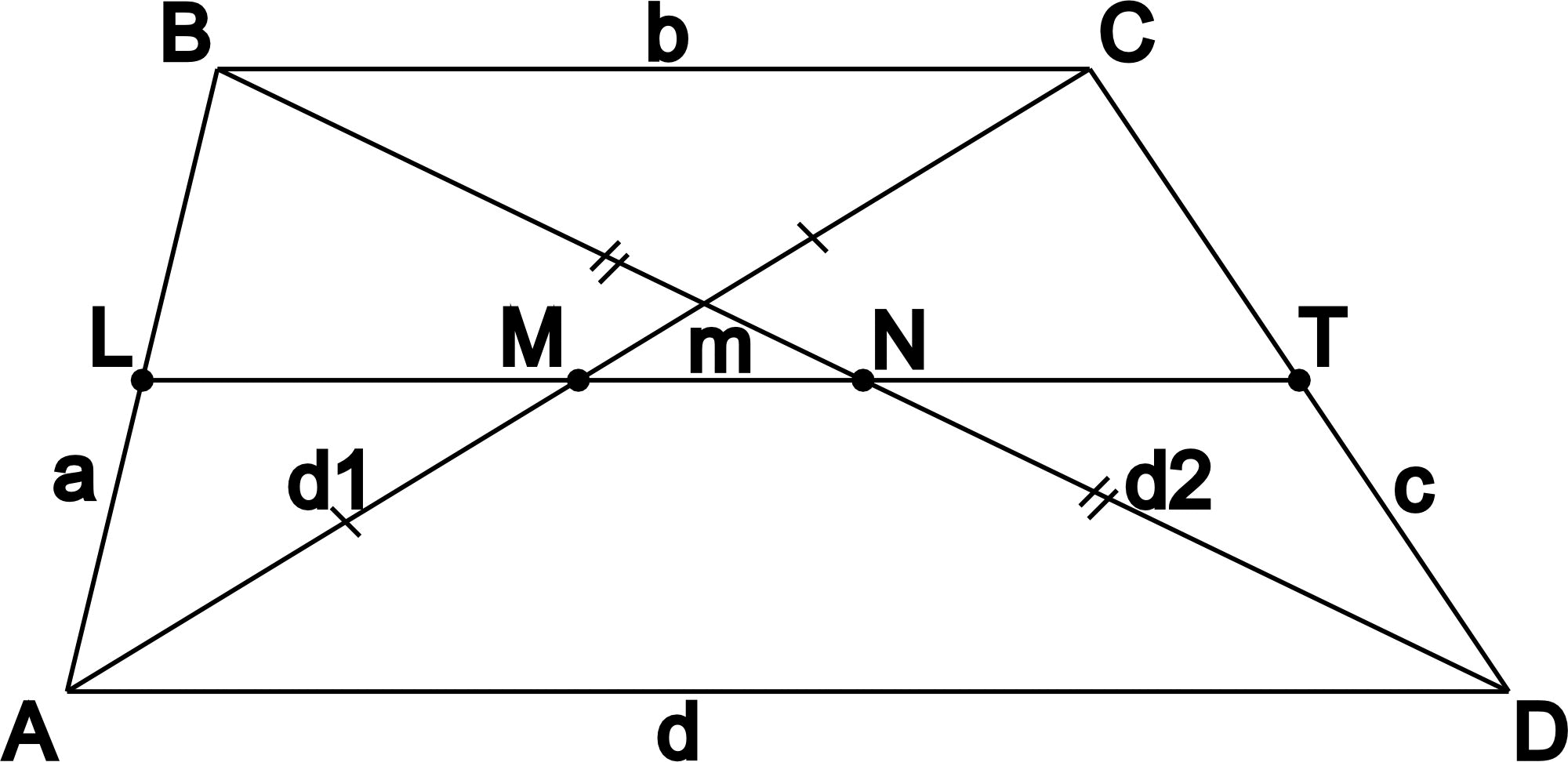
На рисунке d1 и d2 - диагонали трапеции, M и N - точки пересечения диагоналей со средней линией трапеции.
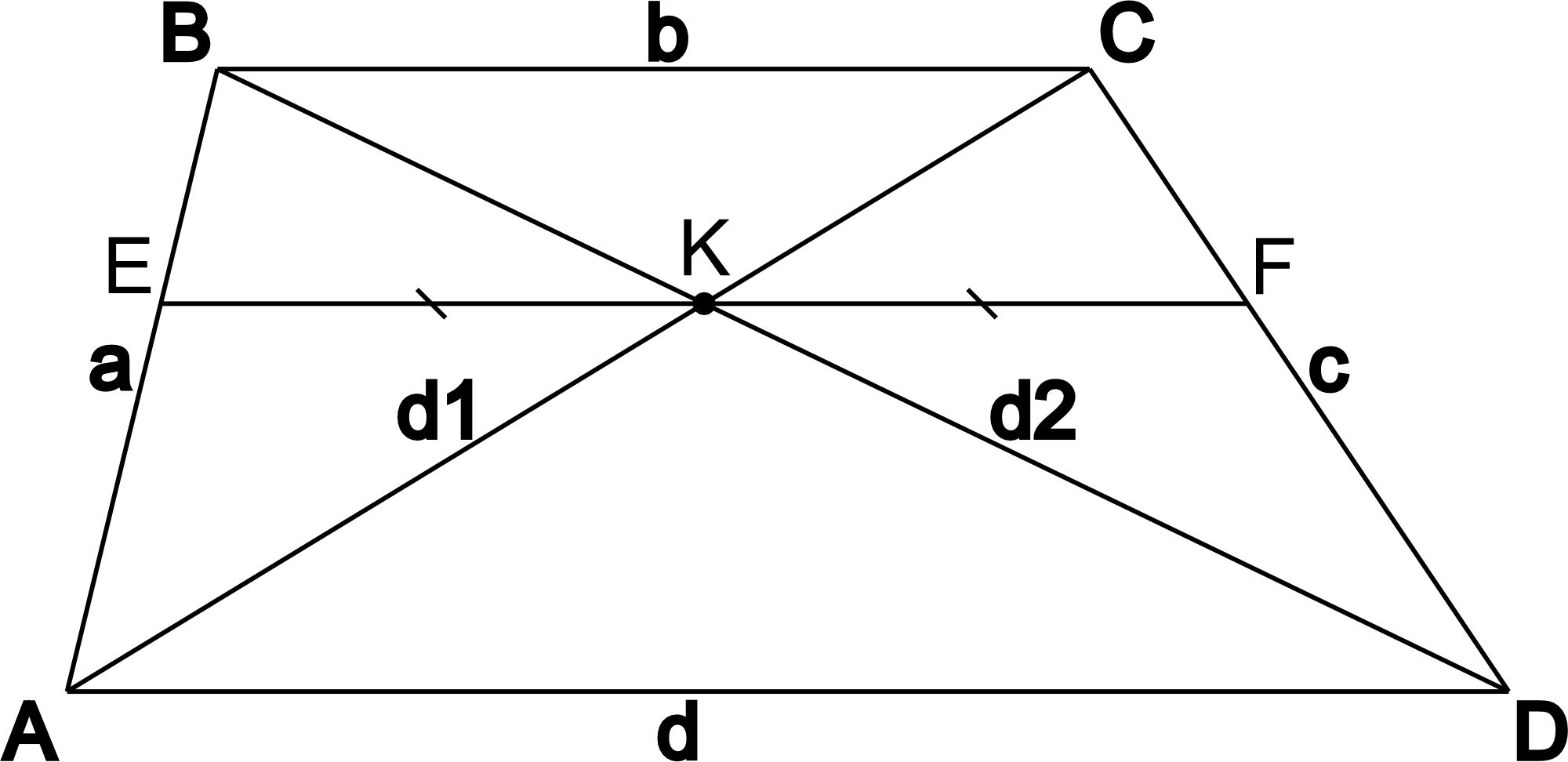
- Отрезок, соеднияющий середины диагоналей равен половине разницы оснований.
- Отрезок, проходящий через точку пересечения диагоналей параллельно основаниям, делится ею пополам:
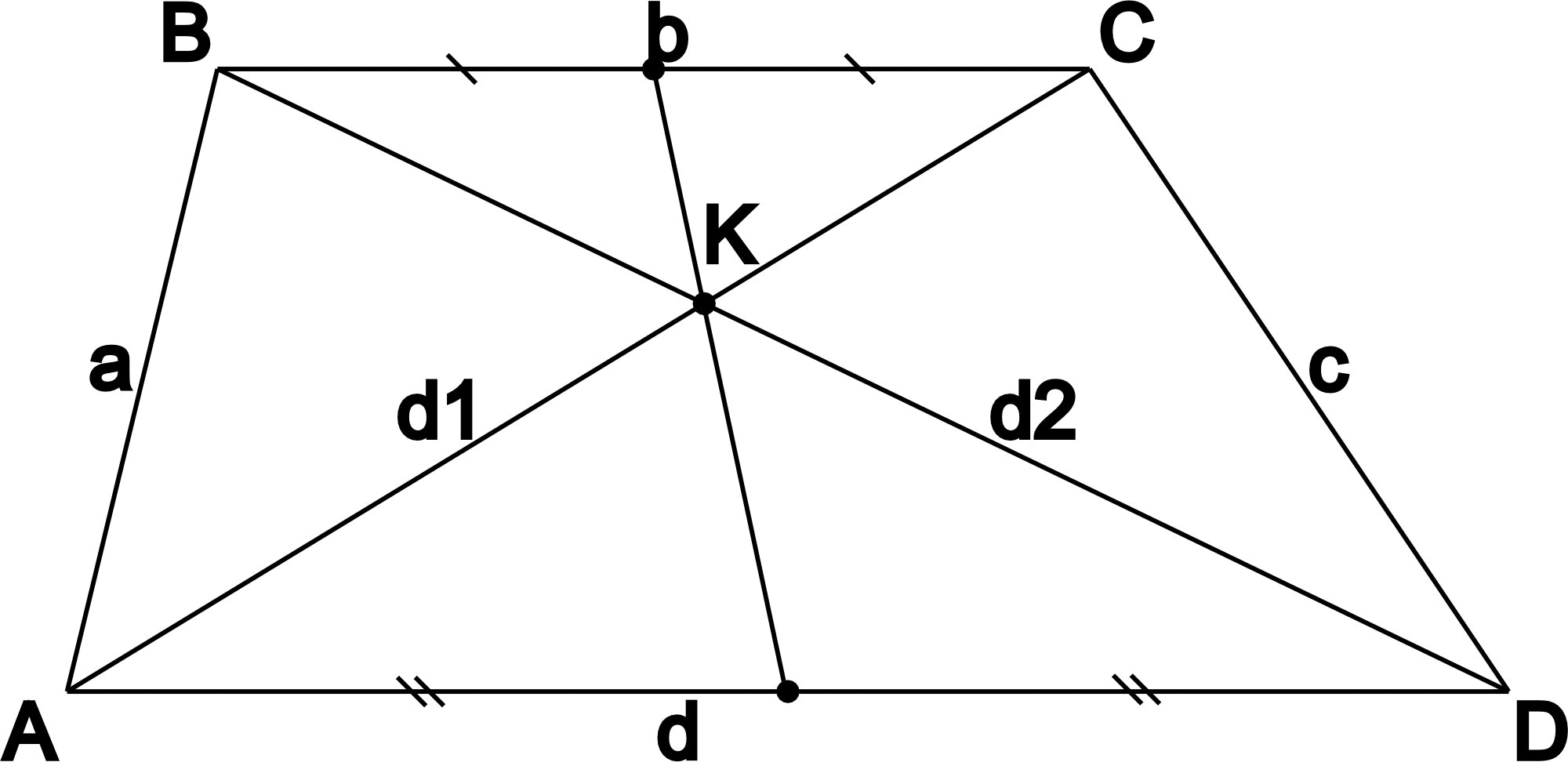
- Точка пересечения диагоналей, середины оснований и точка пересечения продолжений боковых сторон лежат на одной прямой.
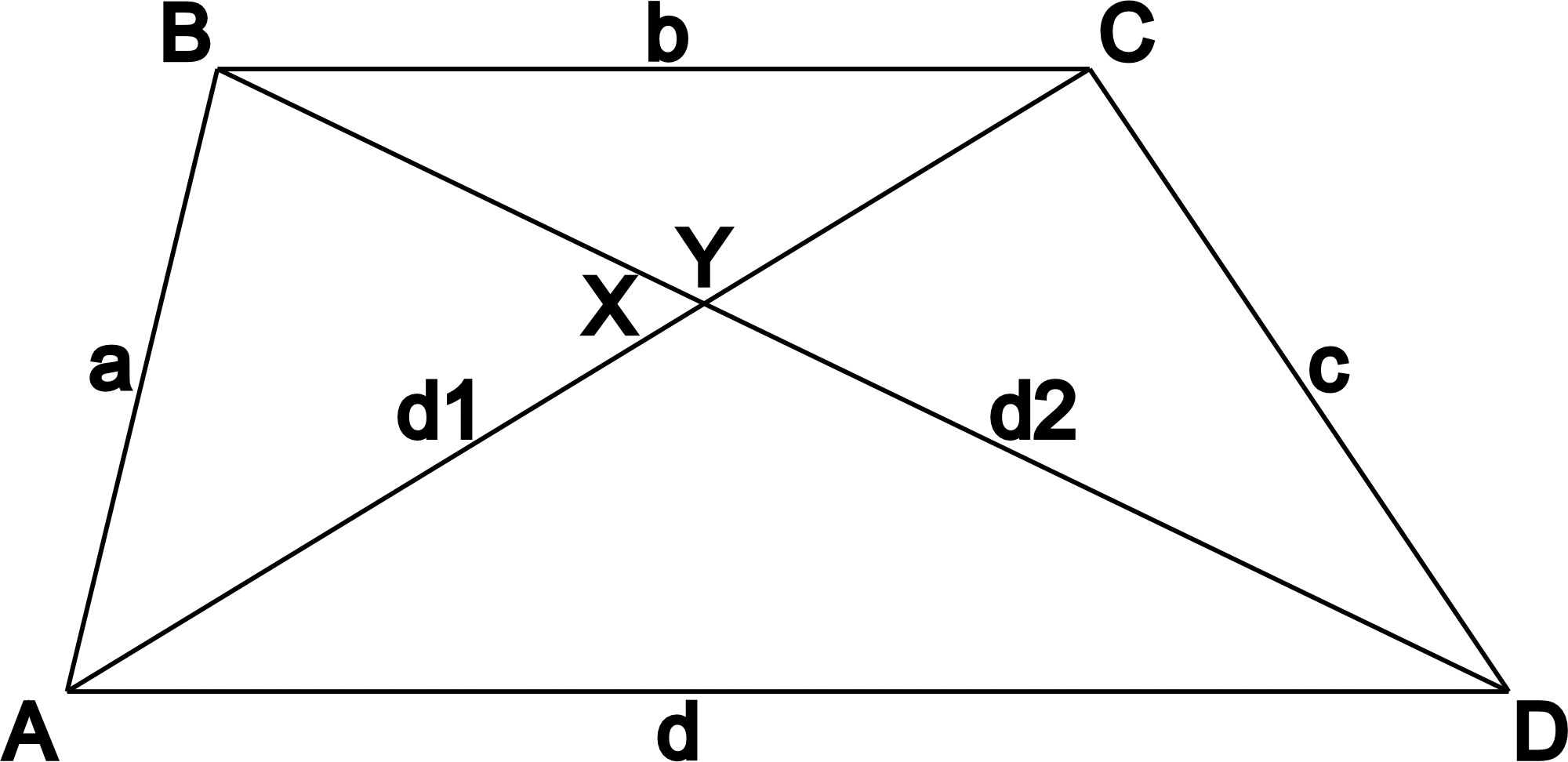
- Диагонали делятся точкой их пересечения в таком же соотношении, как и длины оснований:
- Диагонали делят трапецию на четыре треугольника. Треугольники прилежащие к основаниям - подобные. Треугольники же прилежащие к боковым сторонам имеют одинаковую площадь, то есть являются равновеликими. Если соотношение длин оснований равно k, то соотношение площадей треугольников, прилежащих к основаниям равно k2.
- Диагонали связаны со сторонами следующим соотношением:
Стороны трапеции
Приведём основные формулы вычисления длин сторон трапеции:- Длина основания через длину средней линии и известного основания:
- Длина основания через высоту, длину известного основания и углы при нижнем основании:
- Длина основания через длины боковых сторон и известного основания и углы при основании:
- Длина боковой стороны через прилежащий к ней угол при нижнем основании и высоту:
- Длина основания через длины боковых сторон и диагоналей:
- Длины боковых сторон через длины оснований и диагоналей:
Средняя линия трапеции
Приведём основные формулы вычисления длины средней линии:- Через длины оснований, исходя из четвертого свойства трапеции в данной статье:
- Через площадь и высоту:
Высота трапеции
Высота - это отрезок, соединяющий вершину трапеции и её основание под прямым углом, то есть 90 градусов.Приведём основные формулы вычисления высоты трапеции:
- Через длину боковой стороны и угол при основании прилежащий к ней:
- Через длины диагоналей и оснований и углы между диагоналями:
- Через длины диагоналей и средней линии и углы между диагоналями:
- Через площадь и длины оснований:
- Через площадь и длину средней линии:
- Через длины всех сторон:
Диагонали трапеции
Диагональ - это отрезок, соединяющий противолежащие вершины трапеции.Основые формулы вычисления длин диагоналей трапеции:
- По теореме косинусов:
- Через длины всех сторон:
- Через высоту, длину одного из оснований и один из углов при основании:
- Через соотношение диагоналей и сторон из свойств трапеции:
- Через длины боковых сторон, большего основания и высоту:
Площадь трапеции
Площадь трапеции - это пространство, ограниченное сторонами трапециями, то есть лежащее внутри её периметра.Основные формулы вычисления площади трапеции:
- Через длины оснований и высоту:
- Через длину средней линии и высоту:
- Через длины диагоналей и угол между ними:
- Через длины всех сторон:
Данную формулу следует изпользовать в случае, если b - малое основание, а d - большее и боковая сторона c больше а. В ином случае следует поменять наименования длин сторон в формуле на соответствующие.
- Через формулу Герона для трапеции:
- Через радиус вписанной окружности и угол:
- Если диагонали перпендикулярны друг другу:
Периметр трапеции
Периметр трапеции - это сумма длин всех сторон трапеции. Вычисляется по следующей формуле:Окружность описанная вокруг трапеции
Окружностью описанной вокруг трапеции называется окружность, касающаяся всех вершин трапеции.Напомним, что описать окружность можно только вокруг равнобедренной трапеции. Таким образом приведённая ниже формула применима только в данном случае.
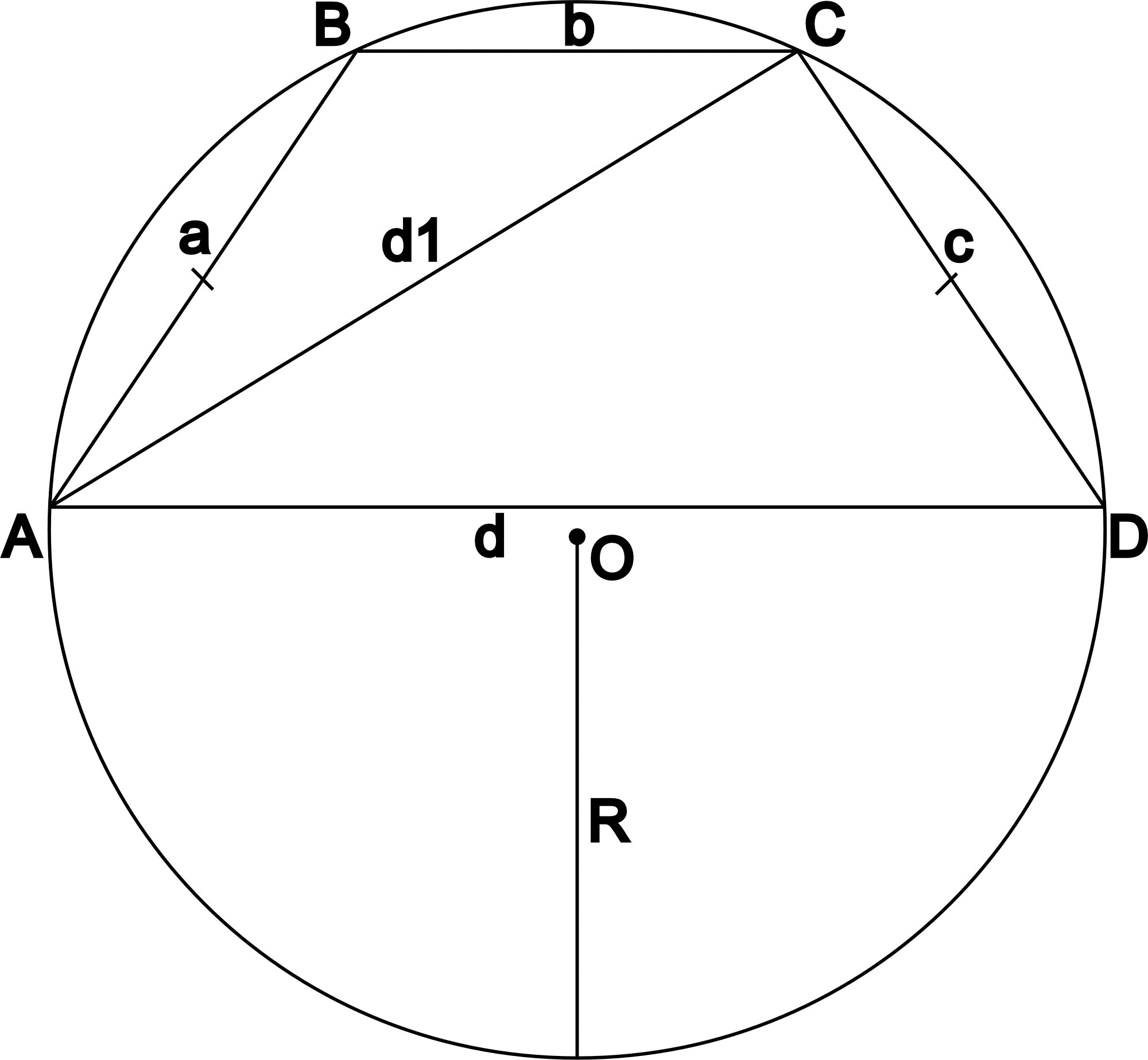
Окружность вписанная в трапецию
Окружностью вписанной в трапецию называют окружность, которая касается всех сторон трапеции.Формула вычисления радиуса вписанной окружности: