Ромб Формулы и свойства
Содержание
- Определение ромба
- Признаки ромба
- Основные свойства ромба
- Стороны ромба
- Диагонали ромба
- Периметр ромба
- Площадь ромба
- Окружность вписанная в ромб
Определение ромба
Ромб - это четырёхугольник, у которого все стороны равны. Ромб всегда является параллелограммом. А частным случаем ромба является квадрат.
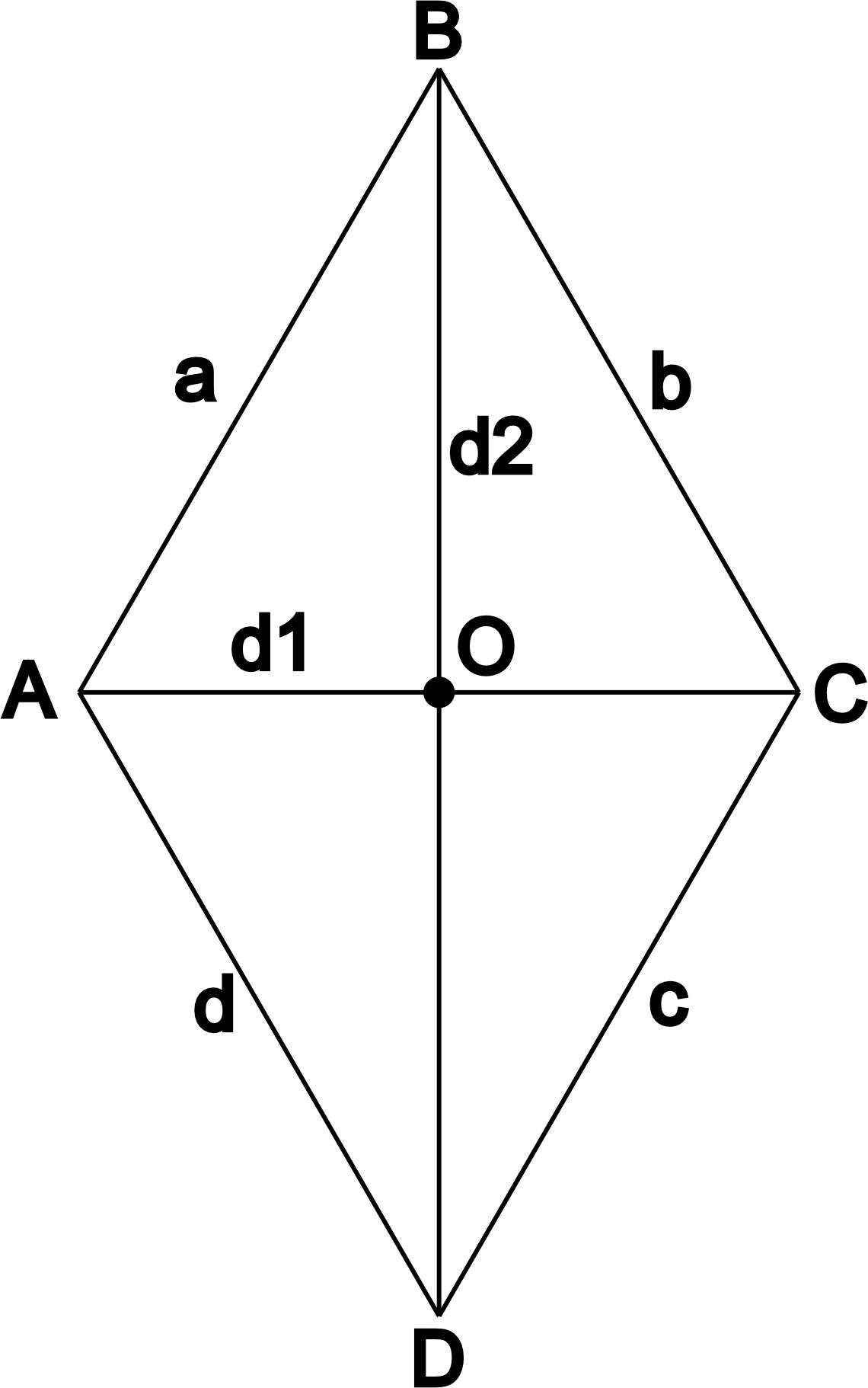
На данном рисунке a, b, c и d - стороны ромба, A, B, C и D - его углы, а d1 и d2 - его диагонали.
Признаки ромба
Так как в общем случае ромб является параллелограммом, описание его признаков отталкивается от частных случаев параллелограмма. Таким образом параллелограмм является ромбом, если:
- Две его смежные стороны равны. Это означает также равенство всех его сторон:
- Его диагонали пересекаются под прямым углом:
- Если одна из его диагоналей является также и биссектрисой угла, из которого она проведена, то есть делит его пополам:
- Если все его высоты равны:
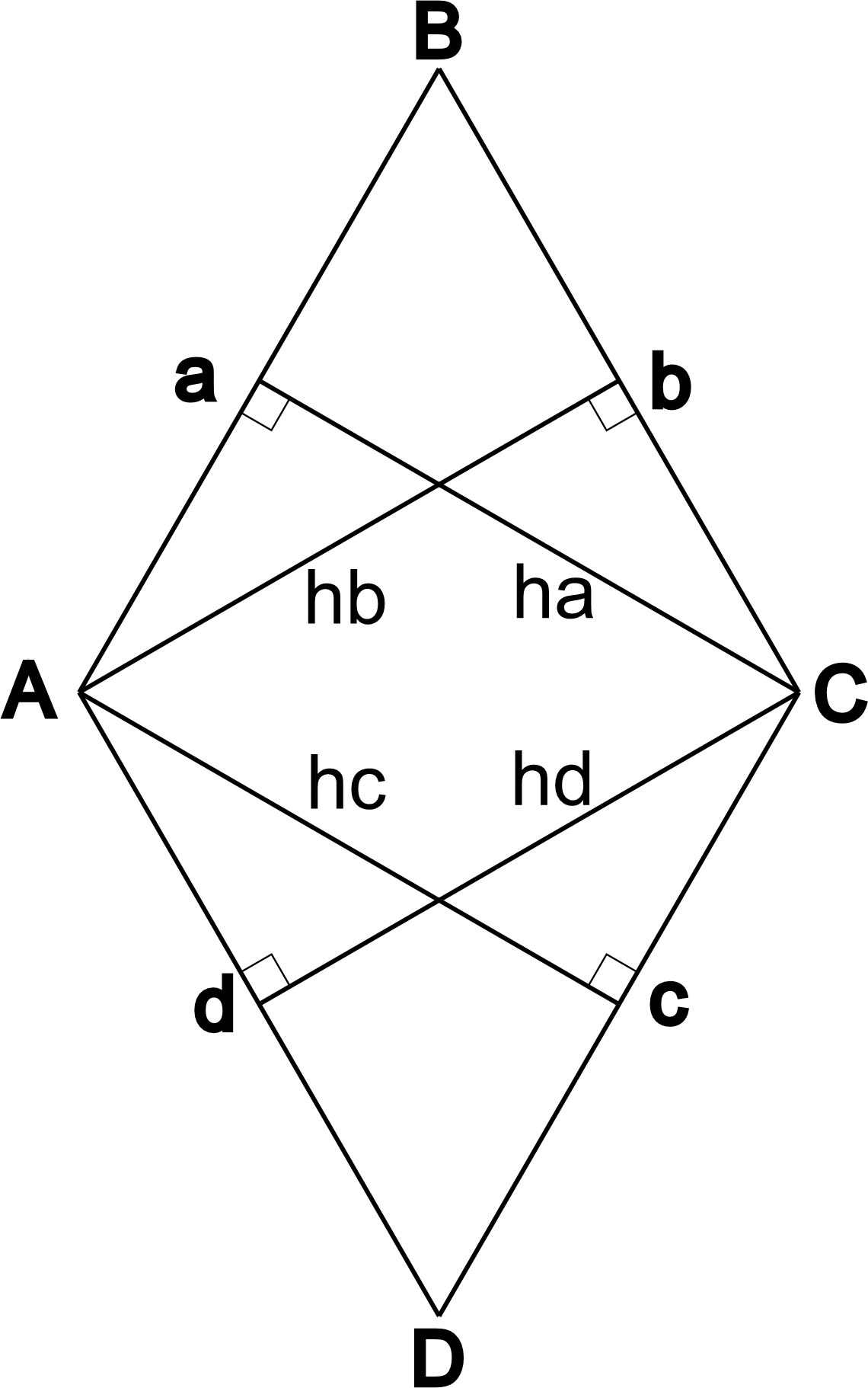
- Если его диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
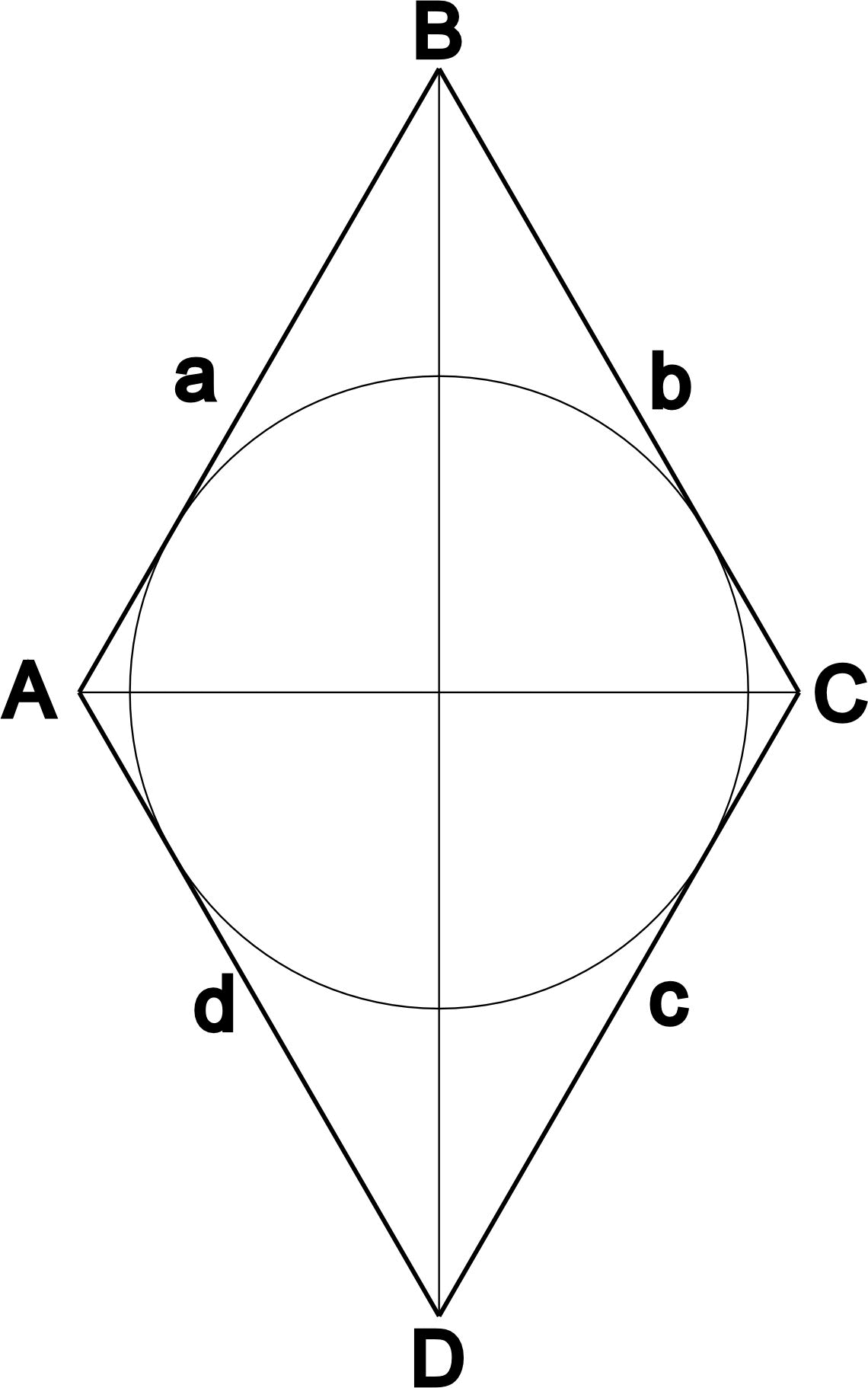
- Если в него можно вписать окружность:
Основные свойства ромба
Так как ромб является параллелограммом, то ему присущи все его свойства. Перечислим их:- Противолежащие стороны равны и попарно параллельны:
- Противоположные углы равны, а сумма углов, прилежащих к одной стороне, равна 180 градусам:
- Все высоты в ромбе равны:
Так как все высоты в ромбе равны, их индексация не несёт смысла и в дальнейшем все высоты в данной статье будут обозначаться h.
- Даигонали ромба перпендикулярны, то есть пересекаются под углом 90 градусов, и делятся точкой их пересечения пополам:
- Диагонали ромба являются биссектрисами его углов, как уже упомяналось в признаках.
- Сумма квадратов диагоналей равна квадрату сторону, умноженному на 4:
- Диагонали являются осями симметрии ромба, а точка их пересечения - её центром.
- Точка пересечения диагоналей является центром вписанной в ромб окружности.
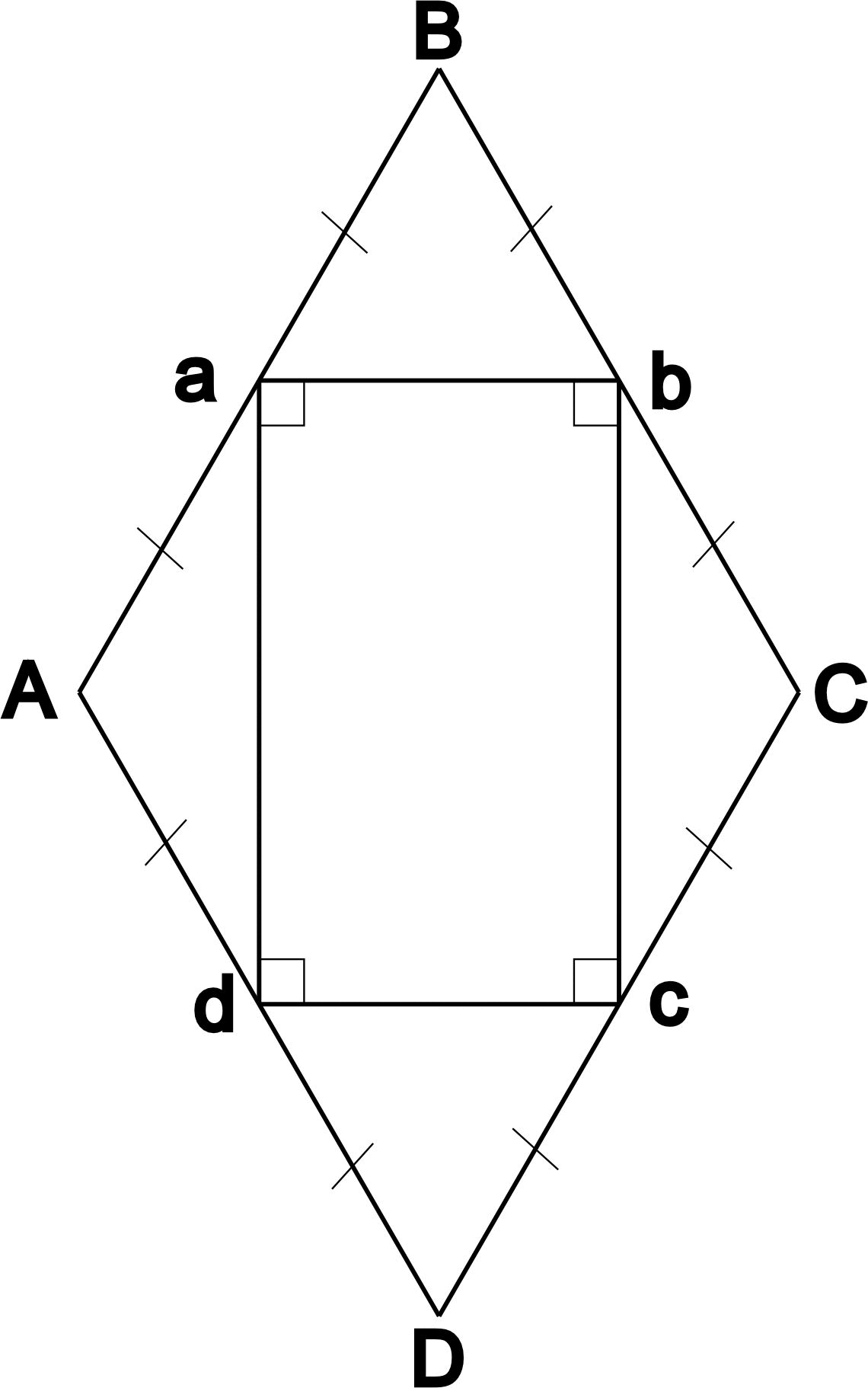
- Середины сторон ромба являются вершинами прямоугольника:
Стороны ромба
Приведём основные формулы, для вычисления длин сторон ромба:- Через площадь и высоту:
- Через площадь и угол:
- Через площадь и радиус вписанной окружности:
- Через длины диагоналей:
- Через длину одной из диагоналей и острый (угол B) или тупой (угол А) угол ромба:
- Через длину большей диагональ и угол:
- Через длину малой диагональ и угол:
- Через периметр:
Диагонали ромба
Диагональ - отрезок, соединяющий две противоположные вершины ромба. Ромб обладает малой (d1) и большой (d2) диагоналями. Приведём основные формулы расчёта длины диагоналей ромба:
- Через длину стороны и угол:
- Через длину стороны и половинный угол:
- Через длину стороны и известной диагонали:
- Через длину известной диагонали и угол:
- Через площадь и длину известной диагонали:
- Через половинный угол и радиус вписанной окружности:
Периметр ромба
Периметром называют сумму длин всех сторон ромба. Существует одна основная формула вычисления периметра ромба:Площадь ромба
Площадью ромба называют пространство, ограниченное сторонами ромба, то есть его периметром. Ниже приведём основные формулы её вычисления:
- Через длину стороны и высоту:
- Через длину стороны и угол:
- Через длину сторону и радиус вписанной окружности:
- Через длины диагоналей:
- Через радиус вписанной окружности и угол:
- Через длину малой диагонали и тупой угол или через длину большей диагонали и острый угол:
Окружность вписанная в ромб
Окружностью вписанной в ромб называется окружность, примыкающая ко всем сторонам ромба. Центром такой окружности является точкой пересечения диагоналей ромба. Приведём основные формулы расчёта радиуса вписанной в ромб окружности:
- Через высоту:
- Через площадь и длину стороны:
- Через площадь и угол:
- Через длину стороны и угол:
- Через длину диагонали и угол, из которого она проведена:
- Через длины диагоналей:
- Через длины диагоналей и стороны: