Прямоугольник Формулы и свойства

Содержание

Определение прямоугольника
Основные свойства прямоугольника
Стороны прямоугольника
Диагональ прямоугольника
Периметр прямоугольника
Площадь прямоугольника
Окружность описанная вокруг прямоугольника
Угол между стороной и диагональю прямоугольника
Угол между диагоналями прямоугольника

Определение прямоугольника

Прямоугольник - это геометрическая фигура, параллелограмм, у которого все углы равны 90 градусов, то есть прямые.

Также можно сказать, что стороны прямоугольника попарно параллельны и равны, так же как и его две диагонали. Помимо этого эти фигуры обладают рядом других интересным свойств.

Прямоугольники являются крайне интересными и важными геометрическими фигурами. Они широко используются в архитектуре, например для расчёта периметра зданий, а также в дизайне и исскустве.Так прямоугольник в минимализме обозначает простоту и сведение исскуства к базовой форме, а в абстрактном стиле создают структуру и баланс в картине. Давайте более детально рассмотрим прямоугольники и их свойства.

Основные свойства прямоугольника

Рассмотрим основные общеизвестные свойства прямоугольника с точки зрения геометрии. Кроме очевидного факта, что углы данной геометрической фигуры прямые, она обладает рядом других свойств:

Противоположные стороны прямоугольника равны.

$A B = C D; A D = B C$

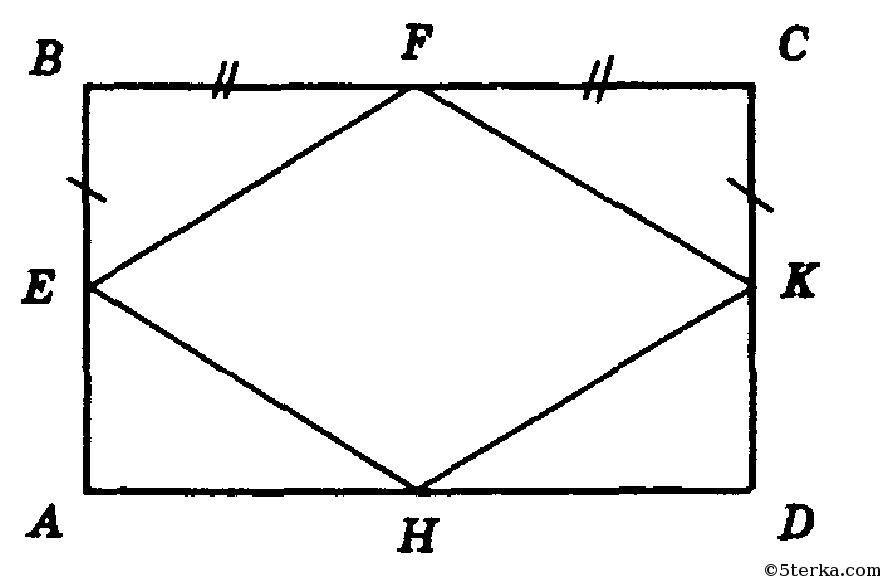
Прямые, проходящие междук серединами сторон прямоугольника образуют ромб.

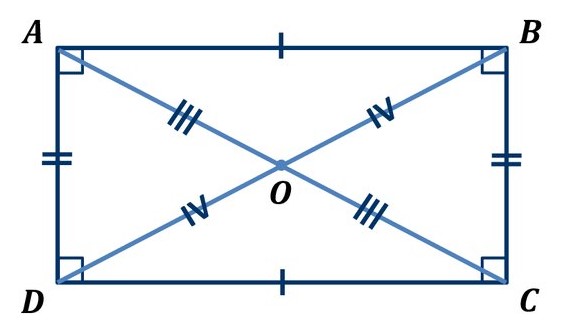
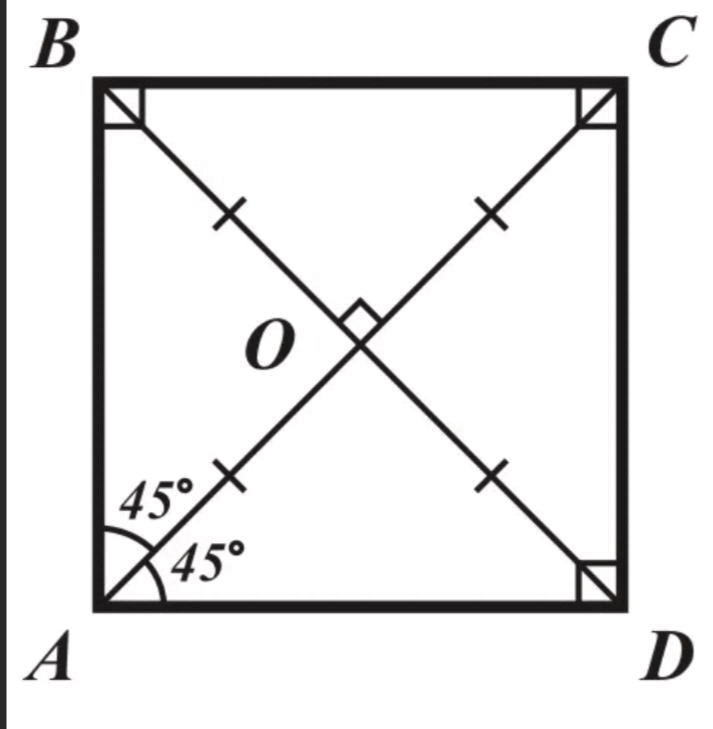
Диагонали прямоугольника всегда равны.

$A C = B D$

Диагонали прямоугольника делятся точкой их пересечения ровно пополам.

$A O = O C; B O = O D$

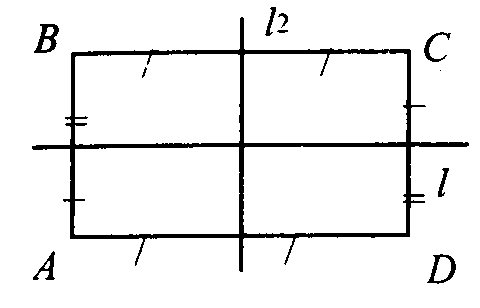
У прямоугольника есть две оси симметрии — это прямые, проходящие через середины противоположных сторон.

Диагонали прямоугольника делят его на два равных прямоугольных треугольника.

$∆ A B C = ∆ A C D; ∆ A B D = ∆ B C D$

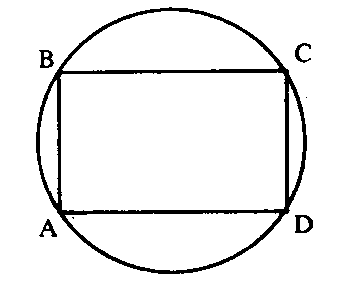
Около любого прямоугольника можно описать окружность, причём диагональ прямоугольника равна диаметру описанной окружности, а точка пересечения этих диагоналей будет являться её центром.

$A C = B D = D_{о к р}$

Изучив данные свойства прямоугольника, мы сможем глубже понять его суть и руководстоваться ими для геометрических расчётов. Как, например, в инженерном деле. При строительстве моста инженеры используют одинаковые прямоугольники для равномерного распределения давления и веса. Это позволяет избежать обрушения моста и одновременно поддерживать движение транспорта, пересекающего его. Инженеры создают долговечную и надёжную инфраструктуру, используя соответствующие прямоугольники.

Стороны прямоугольника

Прямоугольники отличаются между собой только отношением длинной стороны к короткой. Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.
Частным является вид прямоугольника, в котором все стороны равны между собой. В таком случае он будет являться квадратом.

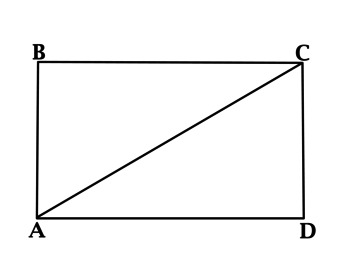
Стоит отметить, что все прямоугольники обладают такой характеристикой, как коэффициент соотношения сторон. Например существует так называемый "золотой прямоугольник". Золотой прямоугольник — это геометрическая форма, в которой отношение более длинной стороны к более короткой стороне равно соотношению всего прямоугольника к более длинной стороне. Такое соотношение примерно равно 1,618 и считается наиболее эстетичным и приятным для человеческого глаза.

Противоположные стороны прямоугольника равны, как нам известно из его свойств.

$A B = C D; A D = B C$

Также стороны прямоугольника являются и высотами данной геометрической фигуры из-за их взаимной перпендикулярности.

Так как прямоугольник является частсным случаем параллелограмма, его противоположные стороны параллельны друг другу.

$A B ∥ C D; B C ∥ A D$

Формулы рассчёта стороны прямоугольника:

Если известны диагональ и одна из сторон. Исходя из того свойства, что диагональ прямоугольника делит его на два прямоугольных треугольника, в которых является гипотенузой, можно применить теорему Пифагора для прямоугольного треугольника для нахождения длин сторон прямоугольника. Это применимо, если известна длина, либо ширина прямоугольника и длина его диагонали. Узнав длину неизвестной стороны, несложно рассчитать длину стороны ей противоположной.

$A B = \sqrt{A C^{2} - B C^{2}}; B C = \sqrt{A C^{2} - A B^{2}}$

$A B = C D; B D = A D$

Если известны периметр и одна сторона. Периметр это сумма длин всех сторон прямоугольника. Таким образом можно найти длину неизвестной стороны, используя следующую формулу:

$A B = \frac{P - 2 B C}{2}; B C = \frac{P - 2 A B}{2}$

$C D = A B; A D = B C$

Если известны площадь и одна сторона. Площадь прямоугольника вычисляется путем перемножения длин его сторон. Исходя из этого факта, расчёт длины неизвестной стороны проводится по следующей формуле:

$A B = \frac{S}{B C}; B C = \frac{S}{A B}$

$C D = A B; A D = B C$

Если известны диаметр описанной окружности и одна сторона. Как следует из свойств прямоугольника, диаметр описанной вокруг него окружности равен длине его диагонали. Тогда преобразуя формулу расчёта по диагонали и длине одной стороны можно приветси к следующему виду:

$A B = \sqrt{{D_{о к р}}^{2} - B C^{2}}; B C = \sqrt{{D_{о к р}}^{2} - A B^{2}}$

$C D = A B; A D = B C$

Если известны диагональ и угол между стороной и диагональю:

$B C = d \times \sin (∠ B A C)$
$A B = d \times \cos (∠ B A C)$

Если известны диагональ и острый угол между диагоналями:

$A B = d \times \sin (\frac{∠ A O B}{2})$
$B C = d \times \cos (\frac{∠ A O B}{2})$

В данном разделе мы поближе познакомились со сторонами прямоугольника, их свойствами и способами расчёта длин. Эта информация широко применяется даже в таких областях, как спорт. Игровые поля для футбола, рэгби и даже тенниса имеют форму прямоугольника с определенным соотношением сторон.

Диагональ прямоугольника

Диагональю прямоугольника называют отрезок, соединяющий две его противоположные вершины, не лежащие на одной стороне. О свойствах диагонали упоминалось в предыдущих разделах, однако продублируем их и в данном для лучшего закрепления. Итак основными свойствами даигонали являются:

Диагональ делит прямоугольник на два равных прямоугольных треугольника
Точка пересечения диагоналей является также точкой пересечения осей и центром симметрии прямоугольника.
Точка пересечения диагоналей является центром описанной вокруг прямоугольника окружности
Длина диагонали равна диаметру описанной вокруг прямоугольника окружности.

Формулы расчёта длины диагонали прямоугольника:

Если известны две стороны. Пользуясь формулой из теоремы Пифагора для прямоугольного треугольника можно произвести расчёт следующим образом:

$d = \sqrt{A B^{2} + B C^{2}} = \sqrt{A D^{2} + C D^{2}}$

Если известны диаметр описанной окружности. Помня. что диагональ прямоугольника и линия диаметра описанной вокруг него окружности совпадают получаем формулу:

$d = D_{о к р} = \frac{R_{о к р}}{2}$

Если известны периметр и одна сторона. Данная формула выводится из первой и формулы расчёта периметра:

$d = \frac{\sqrt{P^{2} - 4 P \times B C + 8 B C^{2}}}{2} = \frac{\sqrt{P^{2} - 4 P \times A B + 8 A B^{2}}}{2}$

Если известны площадь и одна сторона. Данная формула выводится из первой и формулы расчёта площади:

$d = \frac{\sqrt{S^{2} + A B^{4}}}{A B} = \frac{\sqrt{S^{2} + B C^{4}}}{B C}$

Если известны синус угла, который прилегает к диагонали, и длина стороны противолежащей этому углу:

$d = \frac{B C}{\sin (∠ B A C)}$

Если известны косинус угла, который прилегает к диагонали, и длина стороны прилежащей к этому углу:

$d = \frac{A B}{\cos (∠ B A C)}$

В данном разделе мы узнали, как различными способами рассчитать диагональ прямоугольника. Применение этому можно найти в решении множества геометрических и алгебраических задач.

Периметр прямоугольника

Периметр прямоугольника - это сумма длин его сторон. Помня приведенное в прошлых разделах, приведем несколько способов расчёта периметра.

Формулы расчёта периметра прямоугольника:

Если известны две стороны. Зная, что длины противоположных сторон в прямоугольнике равны, получаем следующую формулу:

$P = 2 A B + 2 B C = 2 A D + 2 C D$

Если известны диагональ и одна сторона. Снова применяем к предыдущей формуле теорему Пифагора для прямоугольного треугольникаи получаем слеудющий её вид:

$P = 2 A B + \sqrt{d^{2} - A B^{2}} = 2 B C + \sqrt{d^{2} - B C^{2}} и т . д .$

Если известны диаметр описанной окружности и одна сторона. Выводится из предыдущей формулы простой подстановкой

$P = 2 A B + \sqrt{{D_{о к р}}^{2} - A B^{2}} = 2 B C + \sqrt{{D_{о к р}}^{2} - B C^{2}} и т . д .$

Если известны площадь и одна сторона. Возвращаемся к первой формуле и применяем формулу расчёта стороны через площадь и известную сторону:

$P = 2 A B + 2 \frac{S}{A B} = 2 B C + 2 \frac{S}{B C} и т . д .$

В данном разделе мы ознакомились с понятием периметра прямоугольника и способами его расчёта. Это может быть полезно в области архитектуры, а также в инженерной и научной сфере деятельности для решения разноплановых задач и проблем.

Площадь прямоугольника

Площадь прямоугольника — это мера поверхности фигуры, которая показывает, сколько места она занимает на плоскости. Рассмотрим основные формулы нахождения площади:

Если известны две стороны. Классической формулой вычисления площади прямоугольника является формула, оперирующая длинами сторон прямоугольника:
$S = A B \times B C$
Если известны диагональ и одна сторона. В таком случае вместо длины неизвестной стороны подставляется формула её вычисления через теорему Пифагора для прямоугольного треугольника:
$S = A B \times \sqrt{d^{2} - A B^{2}}$
Если известны периметр и одна из сторон. В данном случае вместо длины неизвестной стороны подставляется формула её вычисления через периметр и известную стороны:
$S = A B \times \frac{(P - 2 A B)}{2}$
Если известны диаметр описанной вокруг прямоугольника окружности и одна из сторон. Как мы помним, диамтер описанной вокруг прямоугольника окружности равен длине диагонали данного прямоугольника. В таком случае всё, что нужно сделать, это подставить значение диаметра описанной окружности в формулу из пункта 2 текущего раздела:
$S = A B \times \sqrt{{D_{о к р}}^{2} - A B^{2}}$

В этом разделе мы познакомились с понятием площади прямоугольника и способами её вычисления. Данная информация может быть использована например в строительстве при расчёте площади загородного участка, либо в дизайнерском деле при планировке комнат в квартире.

Окружность описанная вокруг прямоугольника

Окружность описанная вокруг прямоугольника — это круг, который проходит через четыре вершины прямоугольника, а его центр лежит на пересечении диагоналей прямоугольника. Напомним его основные свойства, упомянутые в прошлых разделах:

Диаметр окружности равен длине диагонали прямоугольника вокург которого она описана.

$D_{о к р} = d$

Центр окружности лежит в точке пересечения диагоналей прямоугольника, вокруг которого она описана.

Исходя из формулы в пункте 1 данного раздела, несложно догадаться, что расчёт диаметра окружности описанной вокргу прямоугольника производится по тем же формулам, что и длины диагонали данного прямоугольника. Приведём упомянутые формулы ещё раз:

Если известны две стороны.

$D_{о к р} = \sqrt{A B^{2} + B C^{2}} = \sqrt{A D^{2} + C D^{2}}$

Если известна диагональ.

$D_{о к р} = d$

Если известны периметр и одна сторона.

$D_{о к р} = \frac{\sqrt{P^{2} - 4 P \times B C + 8 B C^{2}}}{2} = \frac{\sqrt{P^{2} - 4 P \times A B + 8 A B^{2}}}{2}$

Если известны площадь и одна сторона.

$D_{о к р} = \frac{\sqrt{S^{2} + A B^{4}}}{A B} = \frac{\sqrt{S^{2} + B C^{4}}}{B C}$

Если известны синус угла, который прилегает к диагонали, и длина стороны противолежащей этому углу:

$D_{о к р} = \frac{B C}{\sin (∠ B A C)}$

Если известны косинус угла, который прилегает к диагонали, и длина стороны прилежащей к этому углу:

$D_{о к р} = \frac{A B}{\cos (∠ B A C)}$

В данном разделе мы ознакомились со свойствами окружности описанной вокруг прямоугольника, а также с формулами расчёта её диаметра.

Угол между стороной и диагональю прямоугольника

Формулы расчёта угла между стороной и диагональю прямоугольника:

Если известны диагональ и сторона:

$\sin (∠ B A C) = \frac{B C}{d}$
$\cos (∠ B A C) = \frac{A B}{d}$

Если известен острый угол между диагоналями:

$∠ C A D = \frac{∠ A O B}{2}$

Угол между диагоналями прямоугольника

Формулы расчёта угла между диагоналями прямоугольника:

Если известен угол между диагональю и стороной. Используем формулу из предыдущего раздела в обратную сторону:

$∠ A O B = 2 \times ∠ C A D$

Если известны площадь и диагональ:

$\sin (∠ A O B) = \frac{2 S}{d^{2}}$