Параллелограмм Определения и свойства
Содержание
- Определение параллелограмма
- Признаки параллелограмма
- Основные свойства параллелограмма
- Стороны параллелограмма
- Диагонали параллелограмма
- Периметр параллелограмма
- Площадь параллелограмма
Определение параллелограмма
Параллелограмм - это четырёхугольник, в котором противолежащие стороны параллельны, то есть лежат на параллельных прямых.
Рассмотрим частные случаи параллелограмма:
- Ромб - это параллелограмм, в котором все стороны равны.
- Прямоугольник - это параллелограмм, в котором все углы прямые, то есть равны 90 градусам.

- Квадрат - это параллелограмм, в котором все стороны равны и углы прямые.

Признаки параллелограмма
Знание признаков необходимо для выявления параллелограмма среди четырёхугольников.
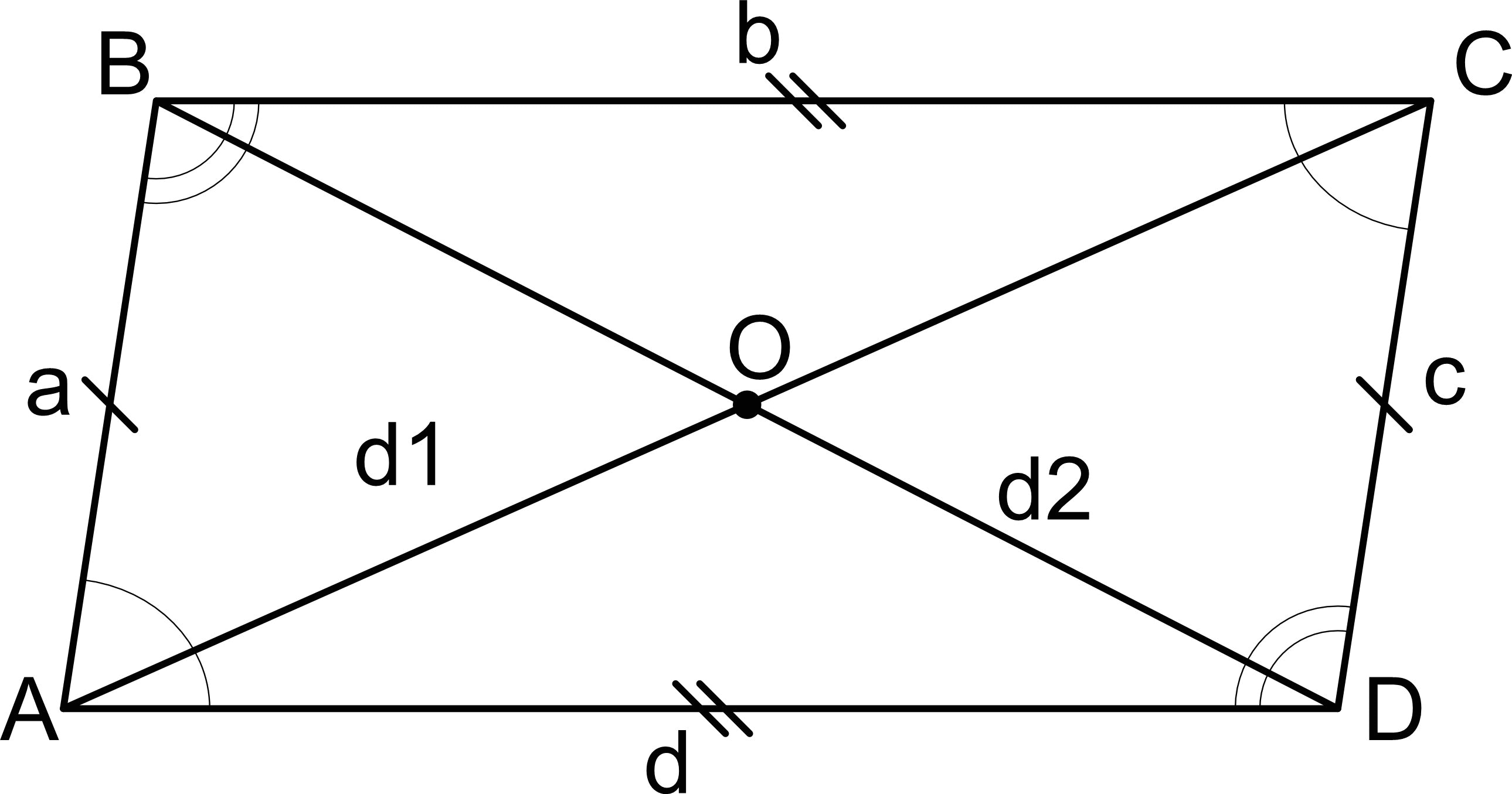
Таким образом четырёхугольник является параллелограммом если:
- Две противоположные стороны параллельны и равны.
- Противоположные стороны четырёхугольника попарно равны.
- Диагонали четырёхугольника пересекаются и точкой их пересечения делятся пополам.
- Протипоположные углы четырёхугольника попарно равны.
- Сумма углов прилежащих к одной стороне равна 180 градусов.
Основные свойства параллелограмма
Нельзя путать свойства параллелограмма и его признаки, приведённые в разделе выше, даже при условии, что они могут повторяться.- Противолежащие стороны параллелограмма равны.
- Противолежащие стороны параллелограмма параллельны.
- Диагонали параллелограмма пересекаются и точкой их пересечения делятся пополам.
- Диагональ делит параллелограмм на два равных треугольника.
- В параллелограмме длины диагоналей и сторон связаны соотношением:
- Сумма углов, прилежащих к одной стороне в параллелограмме, равна 180 градусов.
- Противолежащие углы параллелограмма попрано равны.
- Стороны параллелограмма и высоты опущенные к ним соотносятся следующим образом:
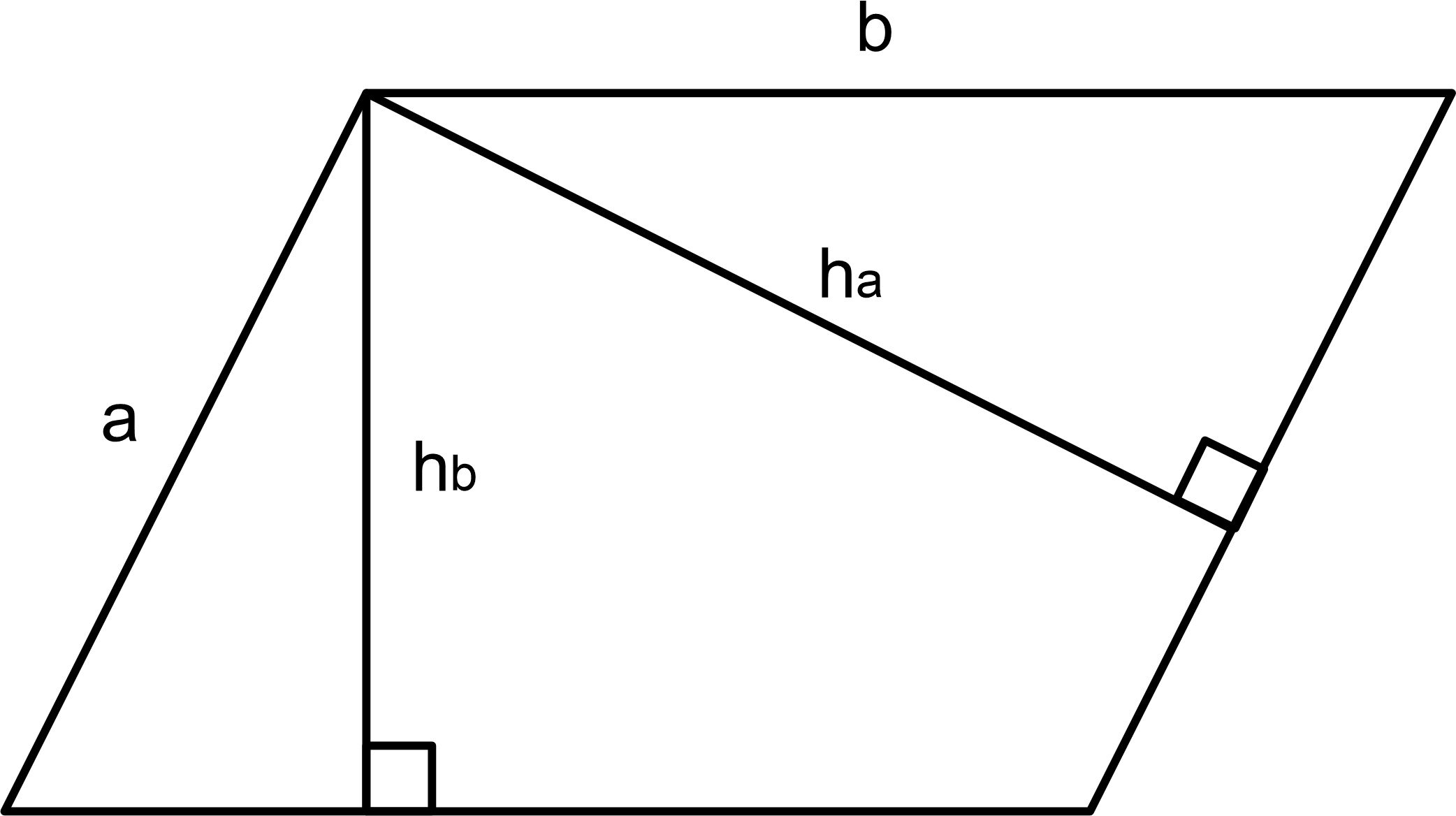
Отдельно остановимся на свойствах биссектрисы в параллелограмме. Бисектриса - это луч, исходящий из вершины угла , делящий его пополам.
- Бисектриса отсекает от параллелограмма равнобедренный треугольник.
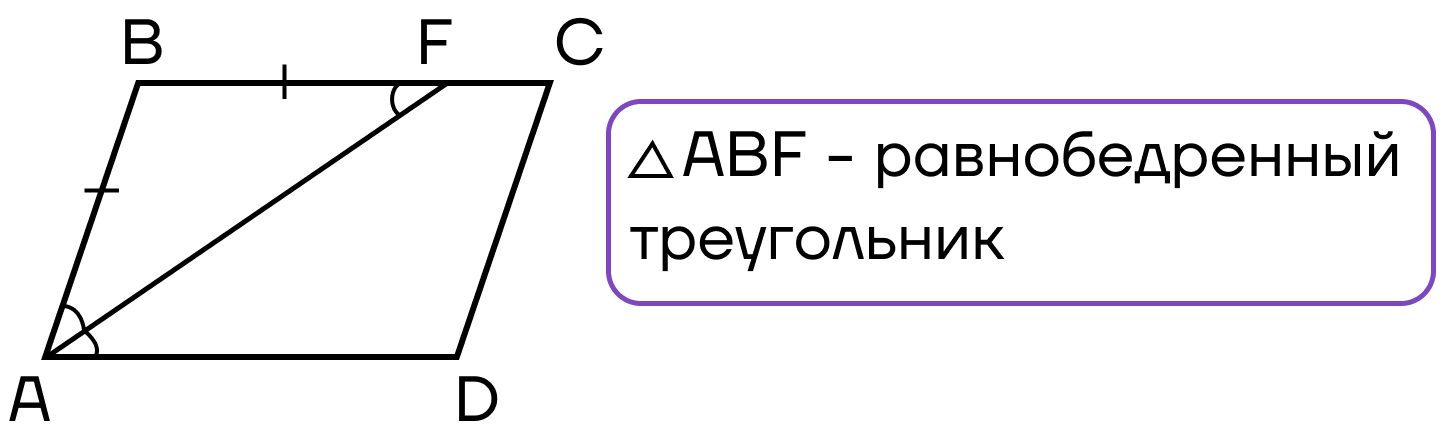
- Бисектрисы, проведенные из уголов прилежащих к одной стороне, образуют между собой прямой угол.
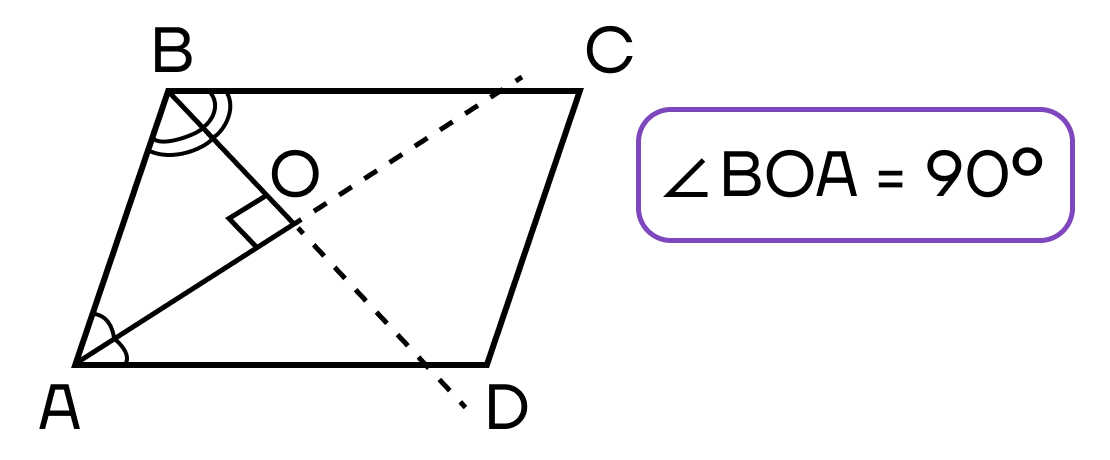
- Отрезки бисектрис противоположных углов равны и параллельны.
Стороны параллелограмма
Формулы для определения длины сторон параллелограмма:- Если известны длины диагоналей и угол между ними:
- Если известны длины диагоналей и одна из сторон:
- Если известны длина высоты и синус угла:
- Если известны площадь и высота:
Диагонали параллелограмма
Диагональ параллелограмма, d1 и d2 - это отрезок, соединяющий две вершины противоположных углов параллелограмма.Формулы для определения длины диагоналей параллелограмма:
- Если известны длины сторон и один из угол:
- Если известны длины сторон и одной из диагоналей:
- Если известны площадь, длина однй из диагоналей и угол между диагоналями:
где и - углы между диагоналями.
Периметр параллелограмма
Периметр параллелограмма, P - сумма длин всех сторон параллелограмма.Формулы определения периметра параллелограмма:
- Если известны длины сторон:
- Если известны длины сторон и двух диагоналей:
- Если известны длина стороны, выстоты и угол:
Площадь параллелограмма
Площадь параллелограмма - часть плоскости, ограниченная сторонами параллелограмма, то есть его периметром.Формулы определения площади параллелограмма:
- Если известны длина стороны и высоты проведённой к ней:
- Если известны длины двух сторон и угол между ними:
- Если известны длины диагоналей и угол между ними: