Эллипс. Формулы и свойства
Содержание
- Определение эллипса
- Элементы эллипса
- Основные свойства эллипса
- Уравнение эллипса
- Радиус круга вписанного в эллипс и описанного вокруг эллипса
- Площадь эллипса и его сегмента
- Приближённая формула периметра эллипса
- Длина дуги эллипса
Определение эллипса
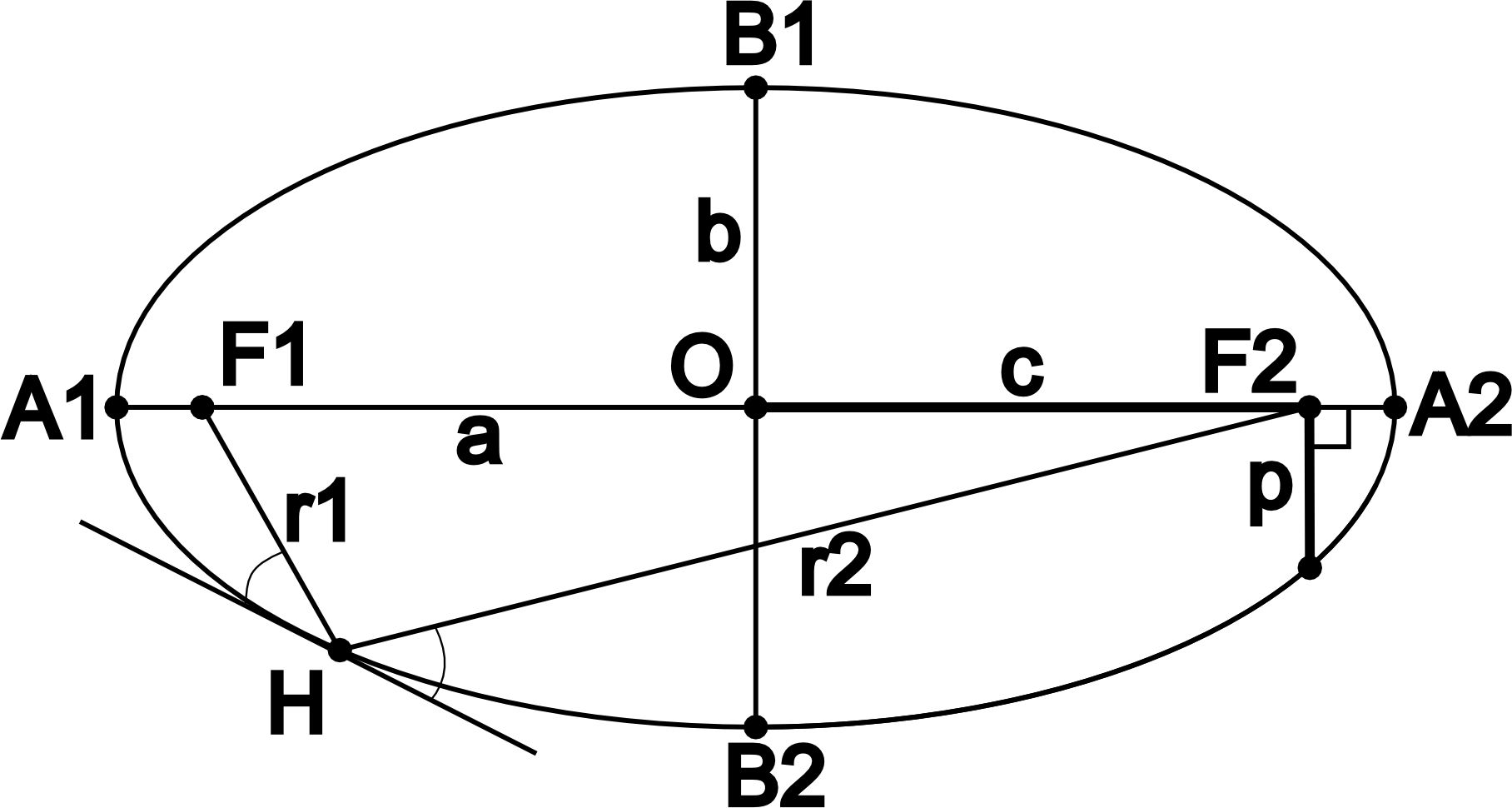
Эллипс - это замкнутая плоская кривая, сумма растояний от любой точки которой до двух точке F1 и F2 является постоянной величиной. Точки F1 и F2 называют фокусами эллипса. Эллипс, в котором фокусы находятся в одной точке, является окружностью. Также в качестве определения эллипса можно использовать следующие формулировки:
- фигура, получаемая в результате афинного преоборазования окружности
- ортогональная проекция окружности на плоскость
- фигура, получаемая в результате пересечения плоскости и прямого кругового цилиндра
Элементы эллипса
Перечислим основные элементы эллипса и их определения:- Большая ось, А - отрезок, концы которого лежат на эллипсе, пересекающий его фокусы. Его длина определяется как 2a.
- Малая ось, B - отрезок, концы которого лежат на эллипсе, пересекающий большую ось под прямым углом и проходящий через центр. Его длина определяется как 2b.
- Большая полуось, a - отрезок, проведенный из центра эллипса к точке его пересечения с большой осью.
- Малая полуось, b - отрезок, проведенный из центра эллипса к точке его пересечения с малой осью.
- Вершины эллипса, A1, А2, В1, В2 - точки пересечения эллипса с большой и малой осями.
- Центр, О - точка пересечения малой и большой оси.
- Диаметр - отрезок, соединяющий две точки эллипса и проходящий через его центр. Диаметры эллипса называются сопряженными, если середины хорд, параллельных первому диаметру лежат на втором диаметре и наоборот.
- Фокальное расстояние, c - расстояние от центра эллипса до его фокуса.
- Эксцентриситет, e - величина, характеризующая вытянутость эллипса. Данная величина может принимать значения [0; 1). Чем ближе она к 1, тем больше эллипс вытянут, а чем ближе к 0, тем он ближе к окружности. Вычисляется по следующей формуле:
- Фокальные радиусы, r1, r2 - расстояния от точки на эллипсе до его фокусов.
- Коэффициент сжатия или эллиптичность, k - отношение длины малой полуоси к большой.
Так как малая полуось всегда меньше большой, коэффициент сжатия эллипса всегда меньше 1. Для окружности же он принимает значение k=1.
Коэффициент сжатия связан эксцентриситетом следующей формулой:
Эллиптичность связана с понятием сжатия эллипса.
- Сжатие, (1-k) - величина, равная разности между единицей и эллептичностью.
- Радиус, R - отрезок, соединяющий точку на элиипсе и его центр. Вычисляется по следующей формуле:
- Фокальный параметр, p - половина длины хорды, проходящей через фокус и перпендикулярной большой оси. Вычисляется по следющей формуле:
- Директриса - прямая, перпендикулярная большой оси эллипса и пересекающая её на расстоянии от центра эллипса. Расстояние от фокуса до директрисы равно . Эллипс обладает двумя директрисами.
Основные свойства эллипса
- Углы между фокальными радиусами и касательной к эллипсу равны (точка H).
- Уравнение касательной к эллипсу в точке H с координатами (Hx;Hy) имеет вид:
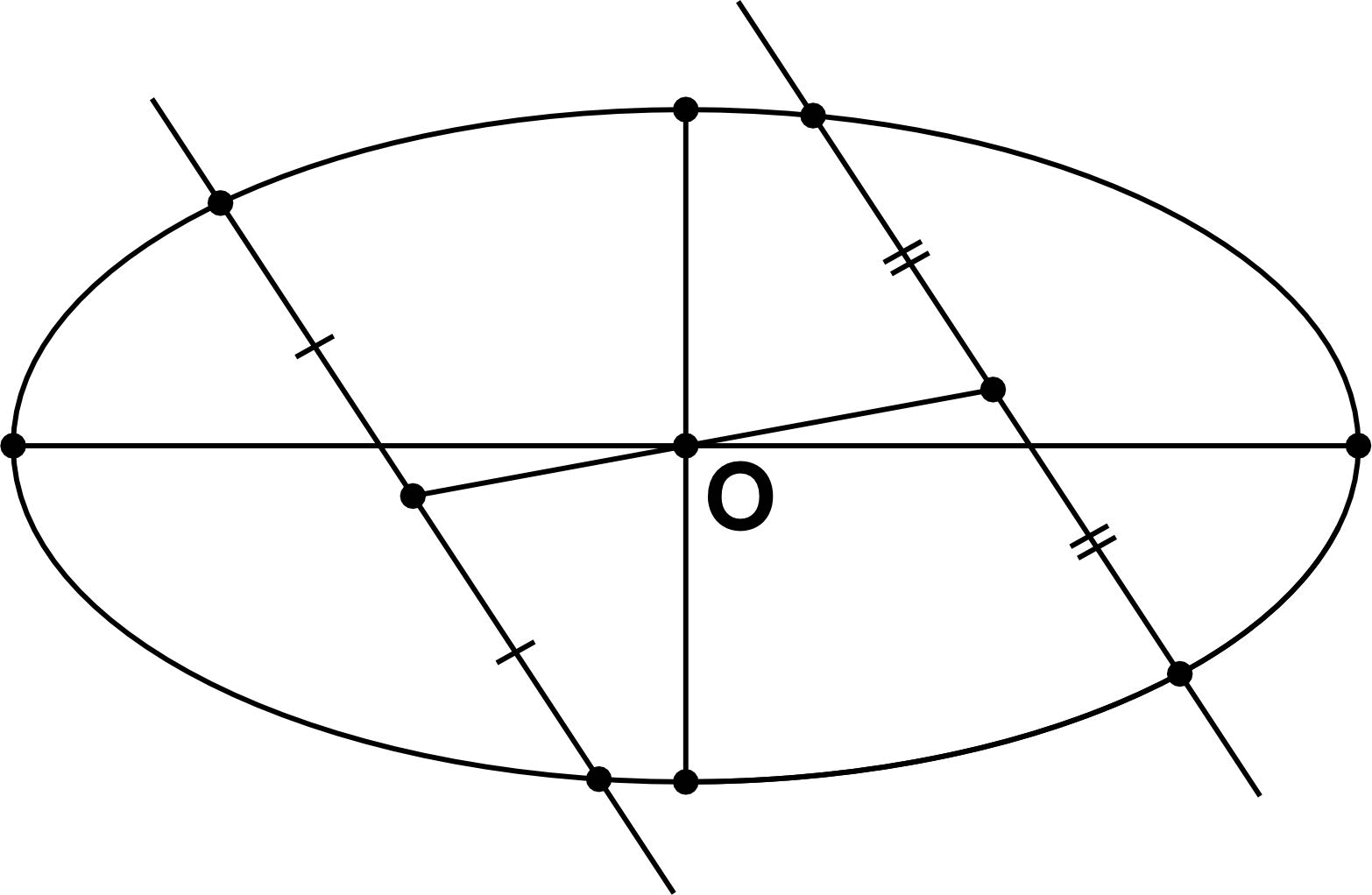
- Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков, образовавшихся в результате пересечения, будет проходить через центр эллипса.
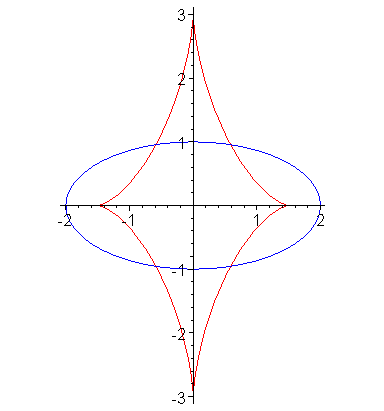
- Эволютой эллипса является астероида, растянутая вдоль малой оси.
- Если вписать эллипс в треугольник АВС, то будет выполняться следующее соотношение:
Уравнение эллипса
Каноническое уравнение:
Такое уравнение описывает эллипс в декартовой системе координат при условии, что центр системы координат находится в центре эллипса, а большая ось лежит на оси абсцисс.
В случае, если центр эллипса смещён относительно центра координат и имеет координаты (x0,y0), то уравнение принимает вид:
Параметрическое уравнение:
Параметр t является углом между положительным направлением оси абсцисс и радиус-вектором данной точки.
Радиус круга вписанного в эллипс и описанного вокруг эллипса
Круг вписанный в элипс касается только двух вершин эллипса: B1 и В2.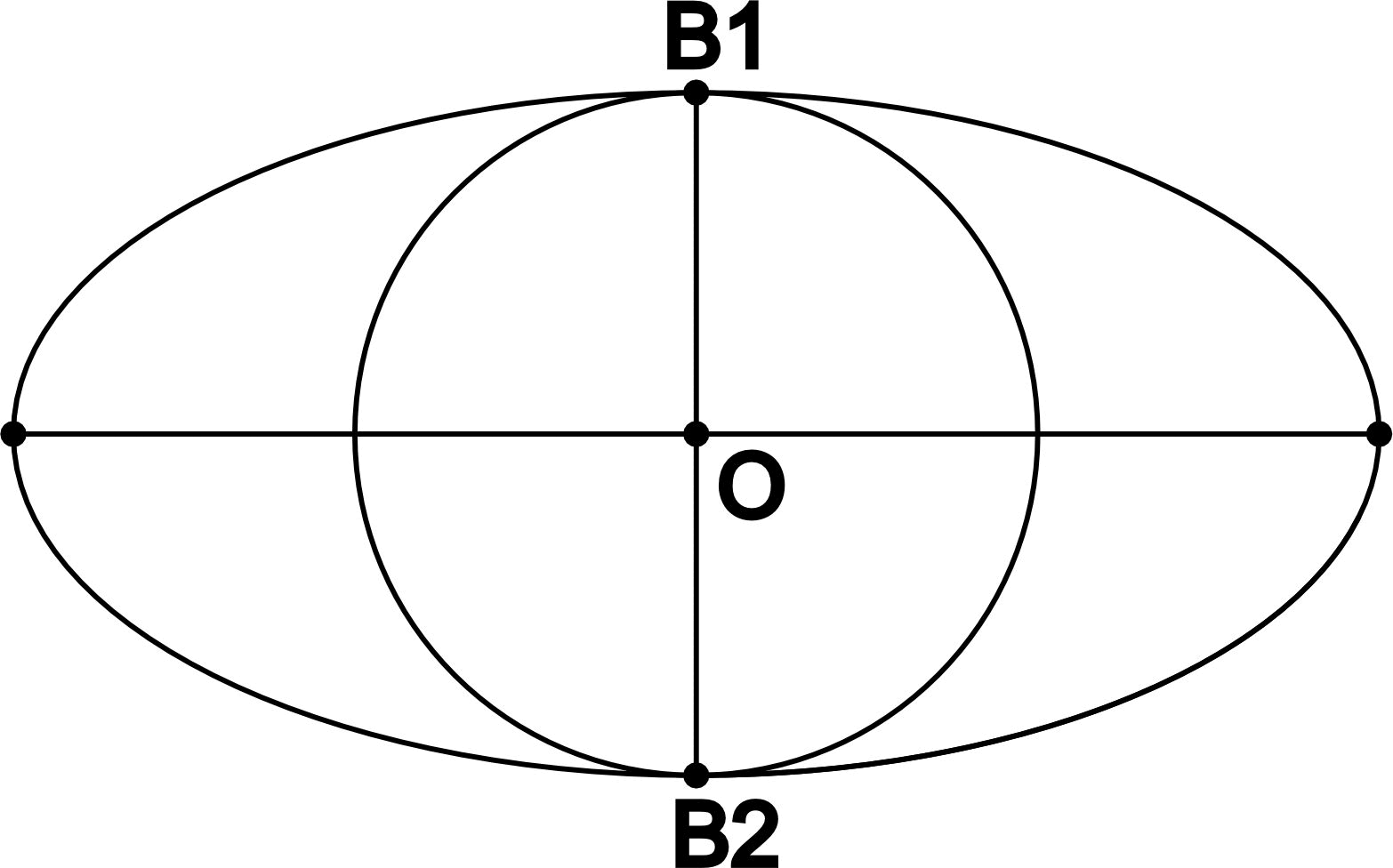
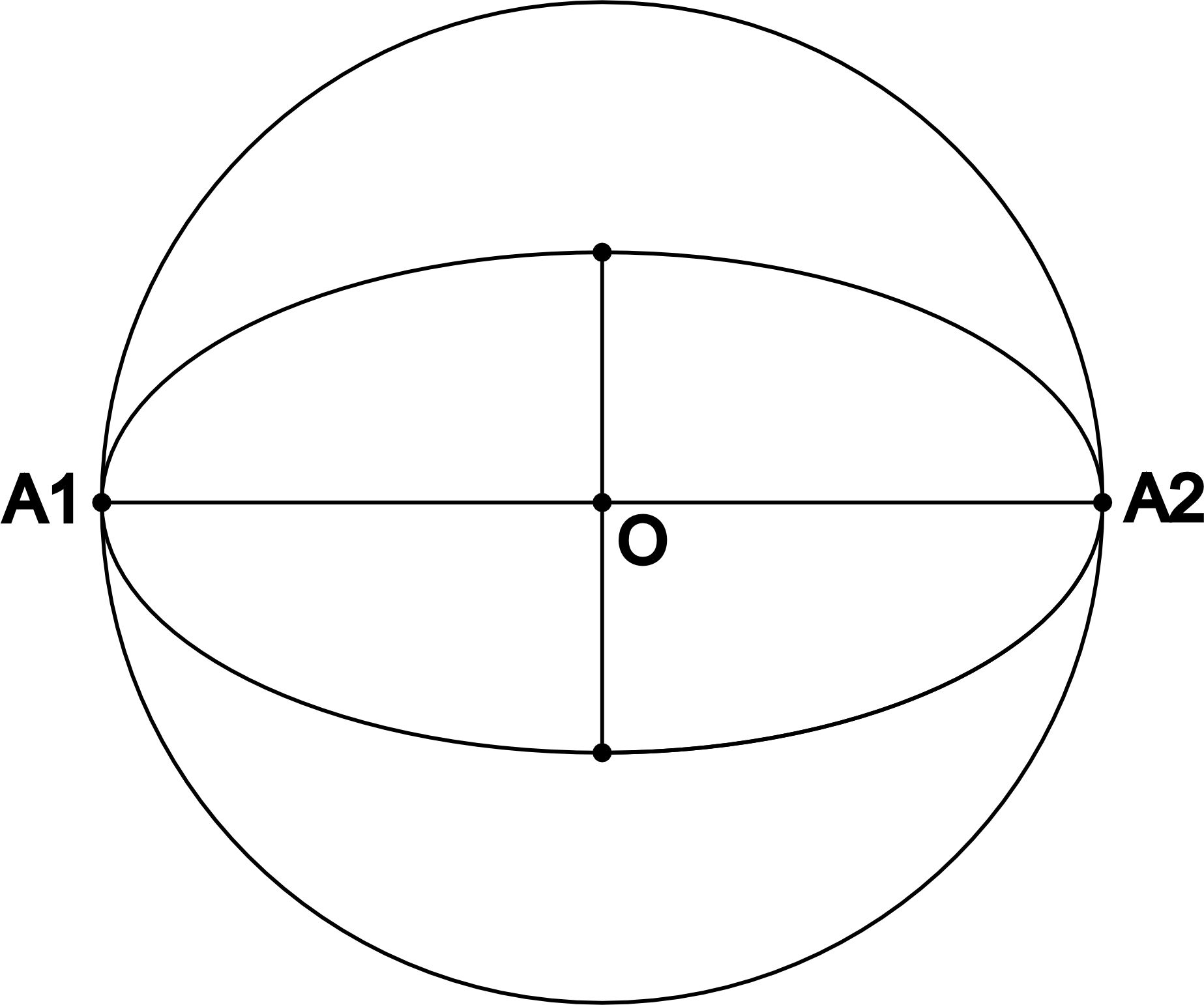
Таким образом его радиус будет равен длине большой полуоси эллипса:
Площадь эллипса и его сегмента
Формула расчёта площади эллипса: Если эллипс задан уравнением Аx2+Bxy+Cy2=1, то площадь можно определить по формуле: Формула площади сегмента, лежащего между дугой выпуклой влево и вертикальной хордой с координатами (x, y) и (x, -y):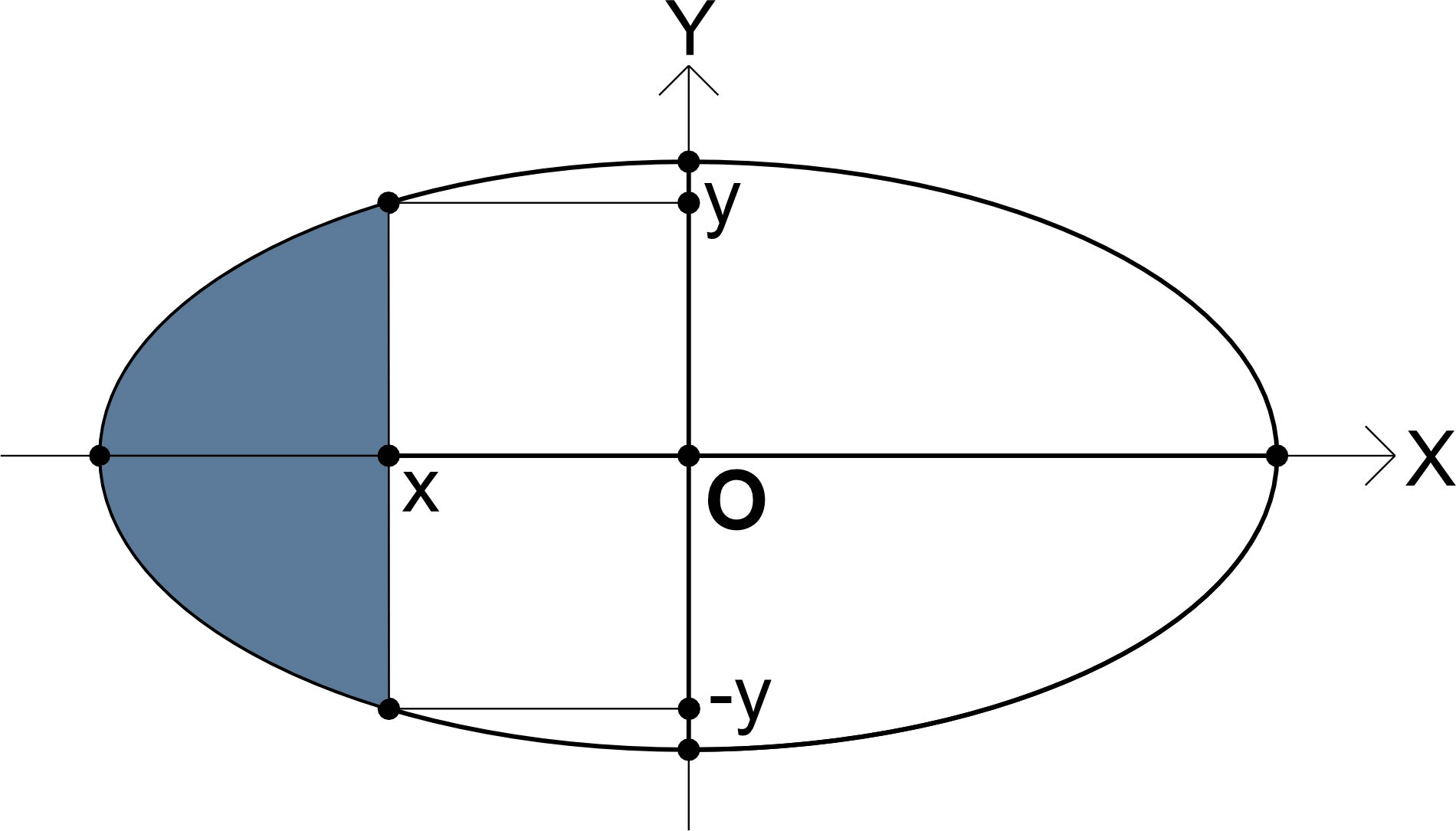
Приближённая формула периметра эллипса
Общей формулы периметра эллипса, L через длины его полуосей с использованием простых функции не существует. Но существует ряд приближённых формул, которые гарантируют определенную точность.
Формула Эйлера:
Другой вариант приближённой оценки длины периметра:
Максимальная поргешность этой формулы 0,63% при эксцентриситете эллипса примерно 0,988. Погрешность всегда положительна.
Погрешность приблизительно в два раза меньше (0,36% при эксцентриситете 0,980) обеспечивает следующая формула: Лучшую точность при 0,05формулы Рамаунджа (0,02%):
Длина дуги эллипса
Параметрическая формула определения длины дуги эллипса через длины полуосей:Выразив длину малой полуоси через длину большой полуоси и эксцентриситет и подставив в предыдущую формул, получим следующую формулу: