Содержание

1. Определение куба
2. Грань куба
3. Ребро куба
4. Вершина куба
5. Центр грани куба и центр куба
6. Ось куба
7. Диагональ куба
8. Диагональ грани куба
9. Объём куба
10. Площадь поверхности куба
11. Периметр куба
12. Сфера вписанная в куб
13. Сфера описанная вокруг куба
14. Свойства куба
15. Координаты вершин куба
16. Единичный куб
17. Пересечение единичного куба  плоскостью

Определение куба

Грань куба

Грань куба (ABCD, EFHG, AEHD и тд) - плоская поверхность, ограниченная сторонами одного из шести квадратов составляющих куб.

• Куб имеет шесть граней, являющихся равными квадратами
• Каждая грань пересекается с четырьмя другими гранями под прямым углом, а оставшейся параллельна
• Грани имеют одинаковую площадь, котороую можно вычислить по формуле для вычисления площади квадрата

Ребро куба

Ребро куба (AB, BC, CD и тд) - отрезок, соединяющий соседние вершины куба и лежащий на пересечении двух его граней. Далее все грани будут обозначаться как a.

• Куб имеет двенадцать рёбер
• Соседние рёбра соединяются друг с другом под прямым углом
• Рёбра имеют одинаковую длину, равную стороне квадрата, являющимся гранью куба

Вершина куба

• Куб имеет восемь вершин
• Каждая вершина образована только тремя гранями и тремя рёбрами

Центр грани куба и центр куба

$O{O}_1=\frac{a}{2}$

Центр куба (О) - точка равноудалённая от всех граней куба. Центр куба лежит на пересечении его диагоналей.

Ось куба

Ось куба (i) - прямая, проходящая через центр куба и центры двух его параллельных граней.

• Куб имеет три оси
• Оси взаимно перпендикулярны

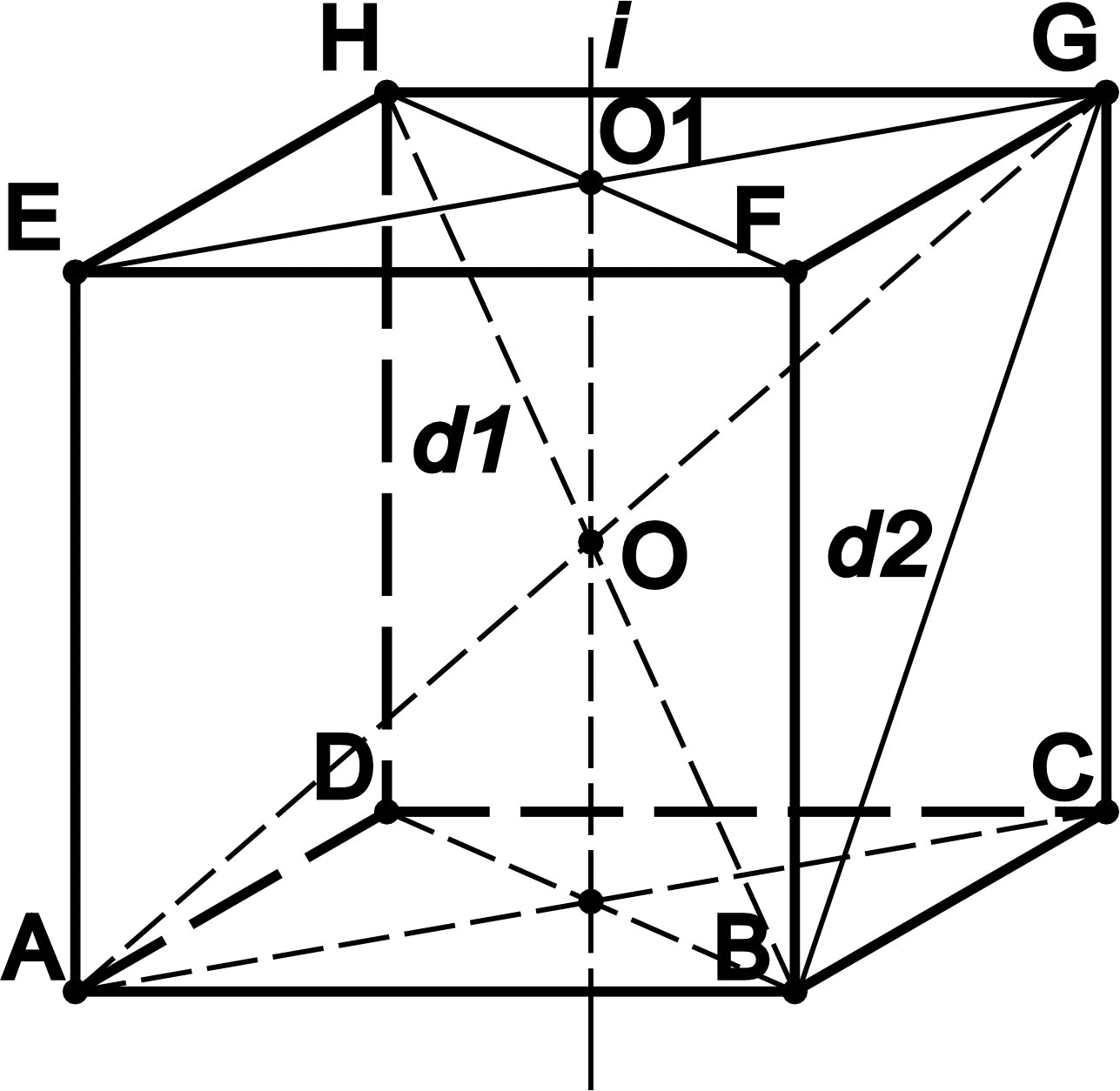
Диагональ куба

Диагональ куба (d₁) - отрезок, соеднияющий две противоположные вершины куба и проходящий через его центр.

• Куб имеет четыре диагонали
• Диагонали куба имеют одинаковую длину
• Диагонали куба пересекаются в центре куба и делятся ею пополам

$OB=OH$

Длину диагонали куба можно вычислить по формуле:

$d_1=a\sqrt{3}$

Диагональ грани куба

Диагональ грани куба (d2) - отрезок, соединяющий противоположные углы грани куба и проходящий через центр грани куба.
Длину диагонали грани куба можно вычислить по формуле:

$d_2=a\sqrt{2}$

Объём куба

Объём куба (V) - совокупность всех точек пространства, ограниченных гранями куба.
Объём куба можно вычислить по следующим формулам:

• Через длину ребра куба:

$V=a^3$

• Через длину диагонали куба:

$V=\frac{{d_1}^3}{3\sqrt{3}}$

• Через длину диагонали грани куба:

$V=\frac{{d_2}^3}{2\sqrt{2}}$

• Через площадь поверхности куба:

$V=\frac{\sqrt{S^3}}{6\sqrt{6}}, где S - площадь поверхности куба$

Площадь поверхности куба

Площадь поверхности куба (S) - сумма площадей всех его шести граней.
Площадь поверхности куба можно вычислить по следующим формулам:

• Через длину ребра куба:

$S=6a^2$

• Через длину диагонали куба:

$S=2{d_1}^2$

• Через длину диагонали грани куба:

$S=3{d_2}^2$

• Через площадь поверхности вписанного в куб шара:

$S=\frac{6S_{щар}}{\mathrm{\pi }}, где S_{шар} - площадь поверхности вписанного шара$

Периметр куба

Периметр куба (P) - сумма длин всех его рёбер.
Вычислить периметр куба можно по следующим формулам:

• Через длину ребра куба:

$P=12a$

• Через длину диагонали куба:

$P=4\sqrt{3}·d_1$

• Через длину диагонали грани куба:

$P=6\sqrt{2}·d_2$

Сфера вписанная в куб

Сфера вписанная в куб - сфера, центр которой совпадает с центром куба, касающаяся всех граней куба.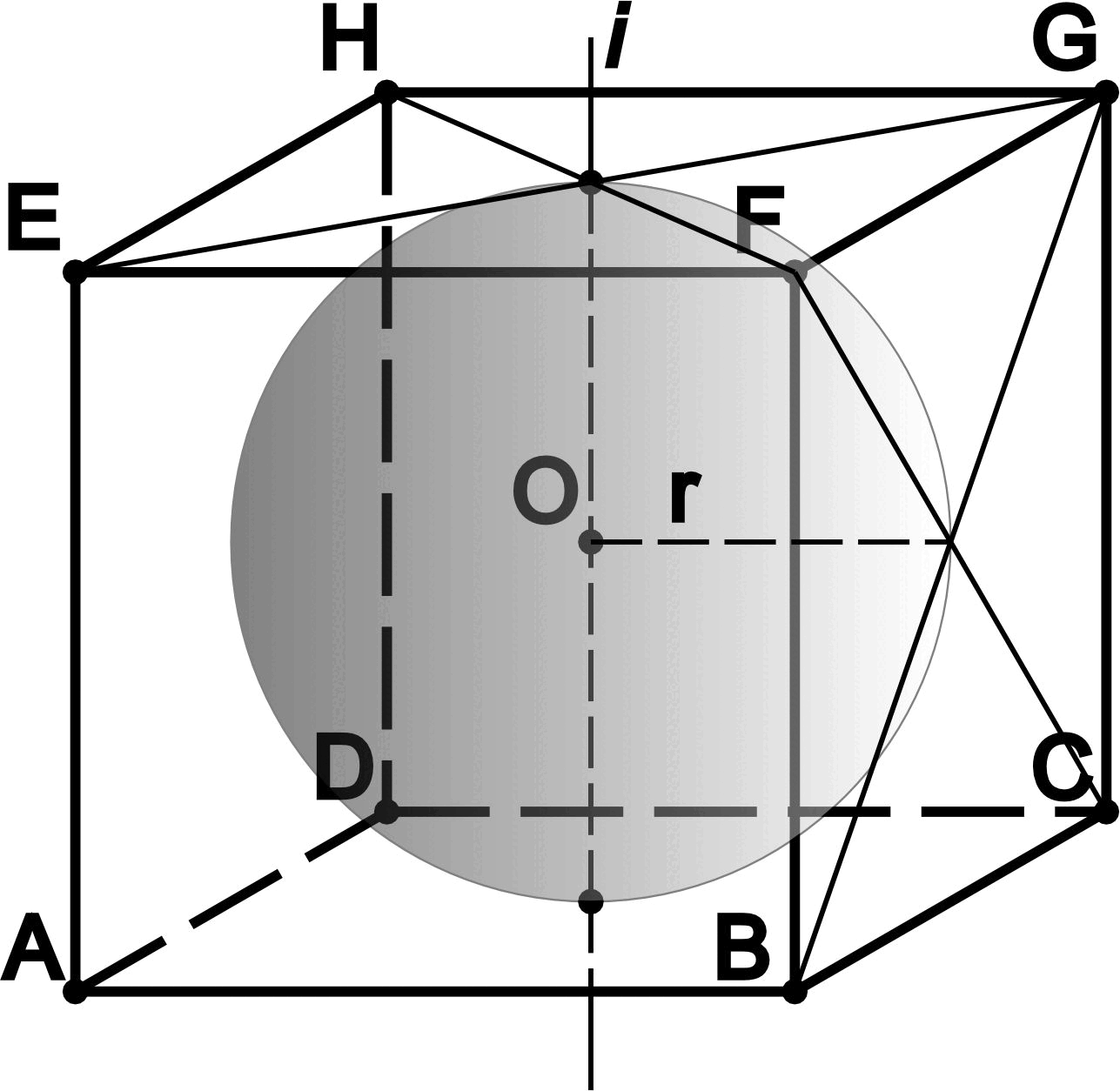

• Все шесть граней куба являются касательными плоскостями к вписанной сфере
• Радиус вписанной сферы (r) равен половине длины ребра куба

$r=\frac{a}{2}$

• Площадь поверхности сферы вписанной в куб (S_{впис.сф.}) через длину ребра куба:

$S_{впис.сф.}=\mathrm{\pi }·{\mathrm{a}}^2$

• Объём сферы вписанной в куб (V_{впис.сф.}) через длину ребра куба:

$V_{впис.сф.}=\frac{\mathrm{\pi }·{\mathrm{a}}^3}{6}$

Сфера описанная вокруг куба

Сфера описанная вокруг куба - сфера, центр которой совпадает с центром куба, касающаяся всех вершин куба.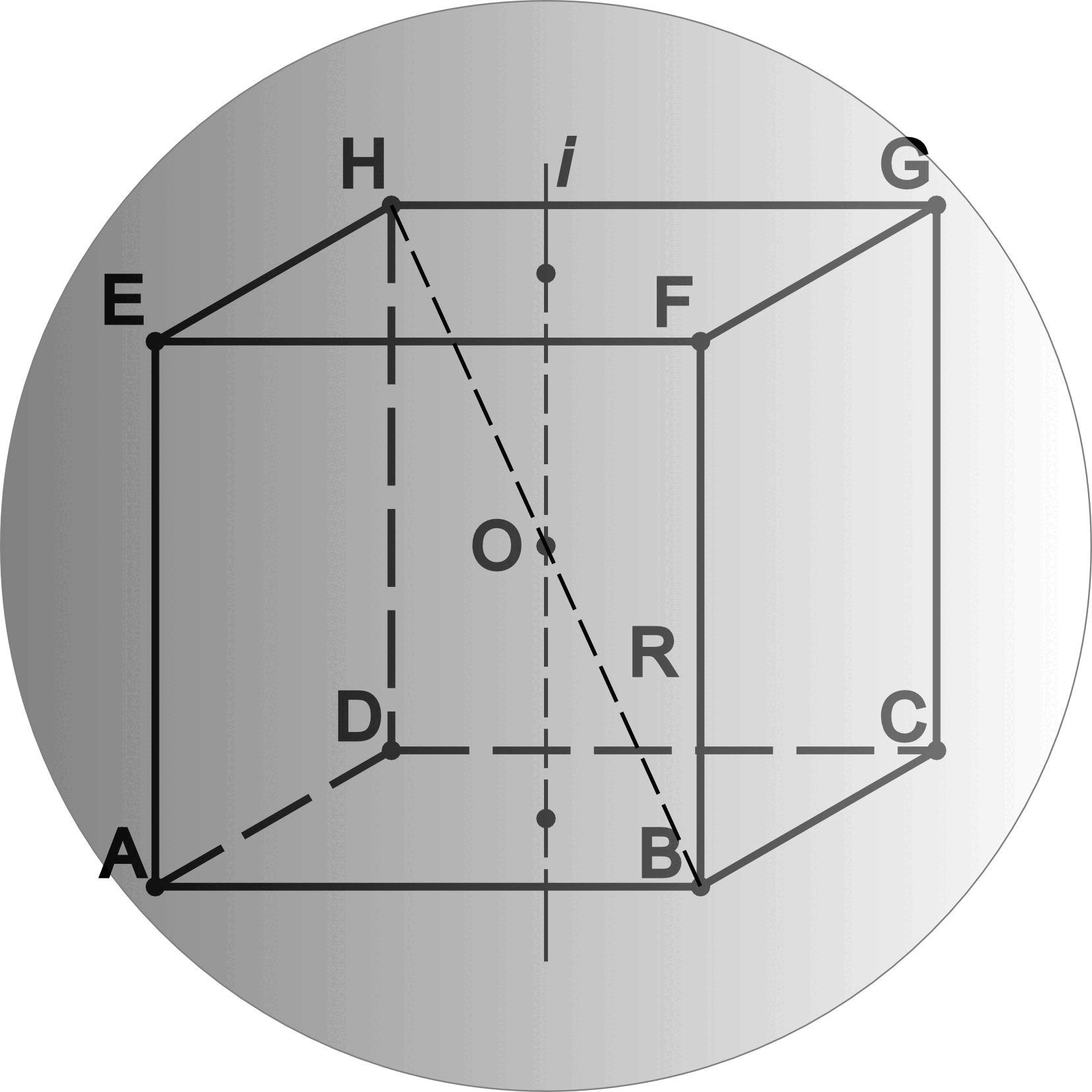

• Радиус описанной сферы (R) через длину ребра куба:

$R=\frac{a\sqrt{3}}{2}$

• Площадь поверхности описанной сферы (S_{опис.сф..}) через длину ребра куба:

$S_{опис.сф.}=3\mathrm{\pi }·{\mathrm{a}}^2$

• Объём описанной сферы (V_{опис.сф.}) через длину ребра куба:

$V_{опис.сф.}=\frac{\mathrm{\pi }·{\mathrm{a}}^3\sqrt{3}}{2}$

Свойства куба

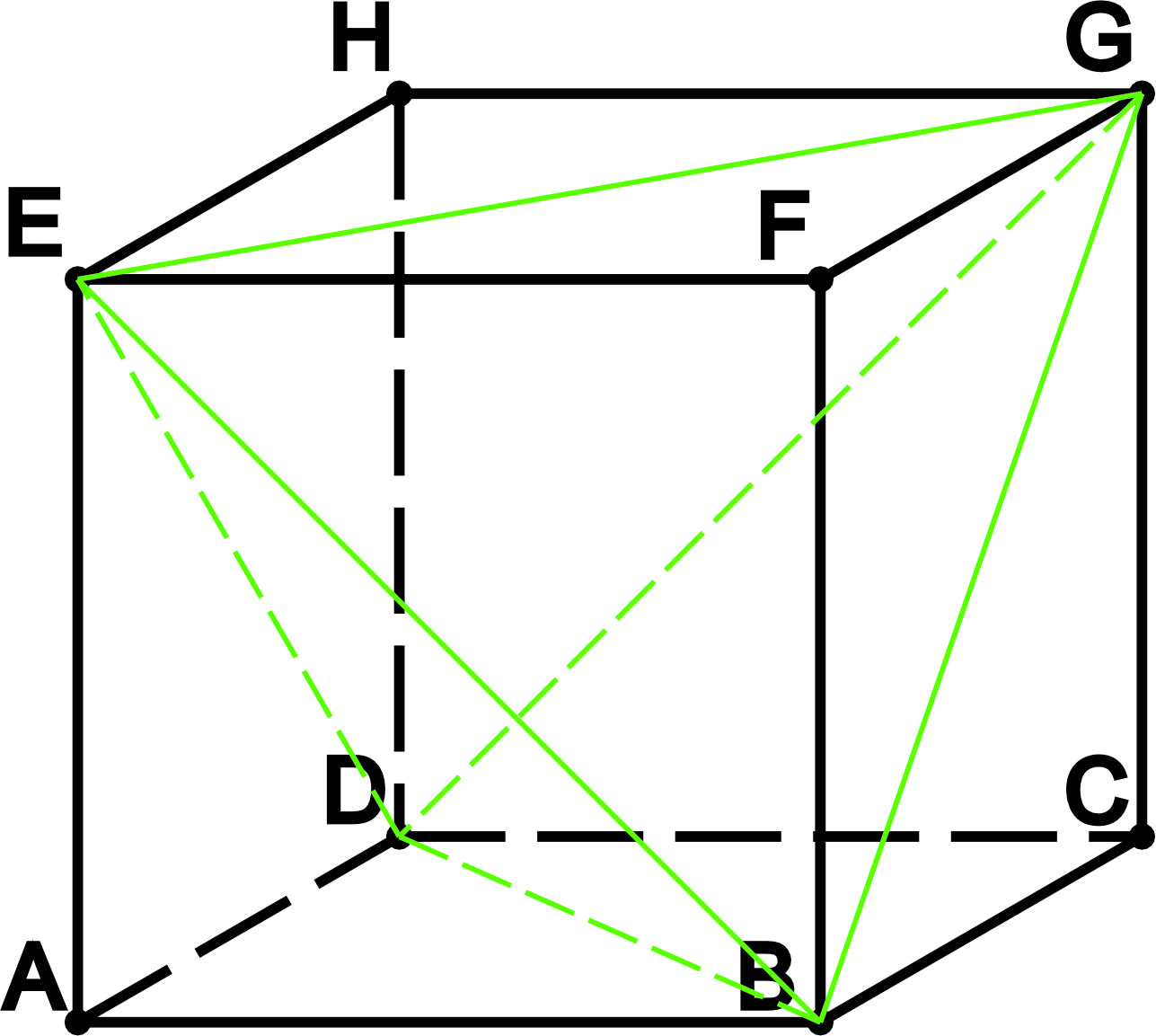
1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырёх вершинах куба, а все шесть рёбер тетраэдра будут лежать на шести гранях куба и рёбра будут равны диагонали грани куба.

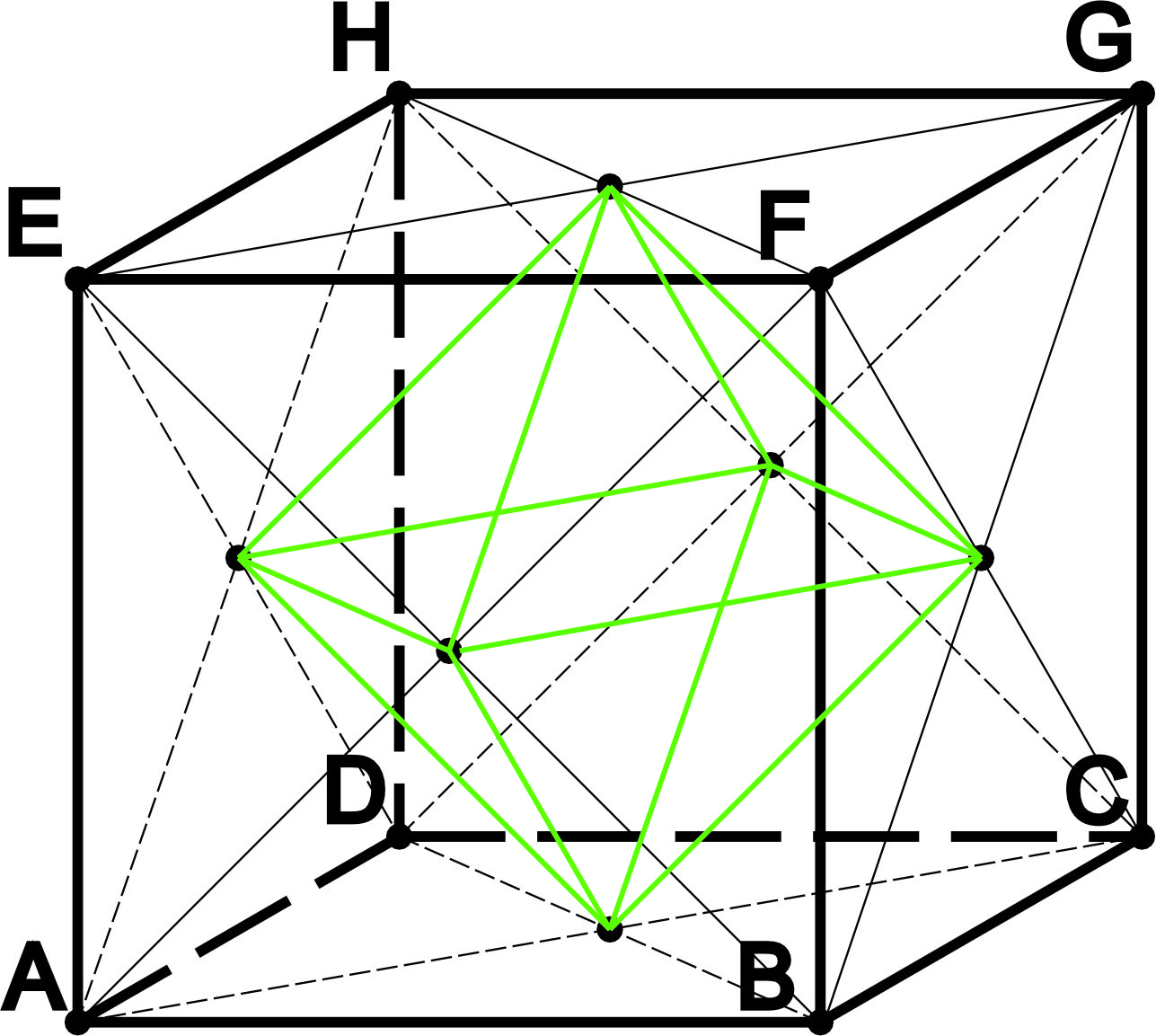
2. В куб можно вписать правильный шекстиугольник так, чтобы все шесть его вершин лежали в центрах граней куба

Координаты вершин куба

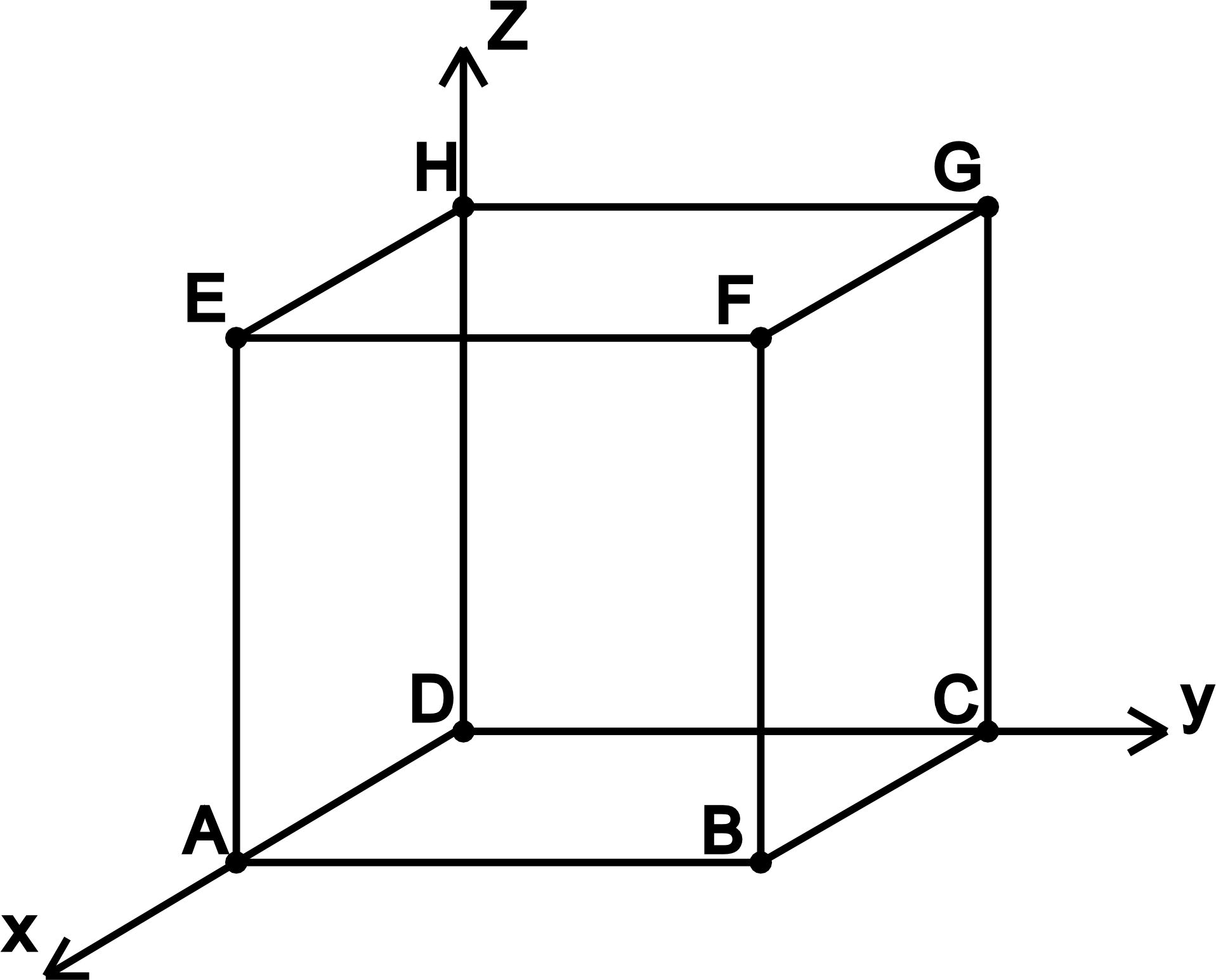
1. Координаты вершин куба со стороной a и вершиной D расположенной в начале декартовой системы координат так, что рёбра этой вершины лежат на осях координат:

$$\begin{gathered} A(a, 0, 0), B(a, a, 0), C(0, a, 0), D(0, 0, 0), \\ E(a, 0, a), F(a, a, a), G(0, a, a), H(0, 0, a). \end{gathered}$$

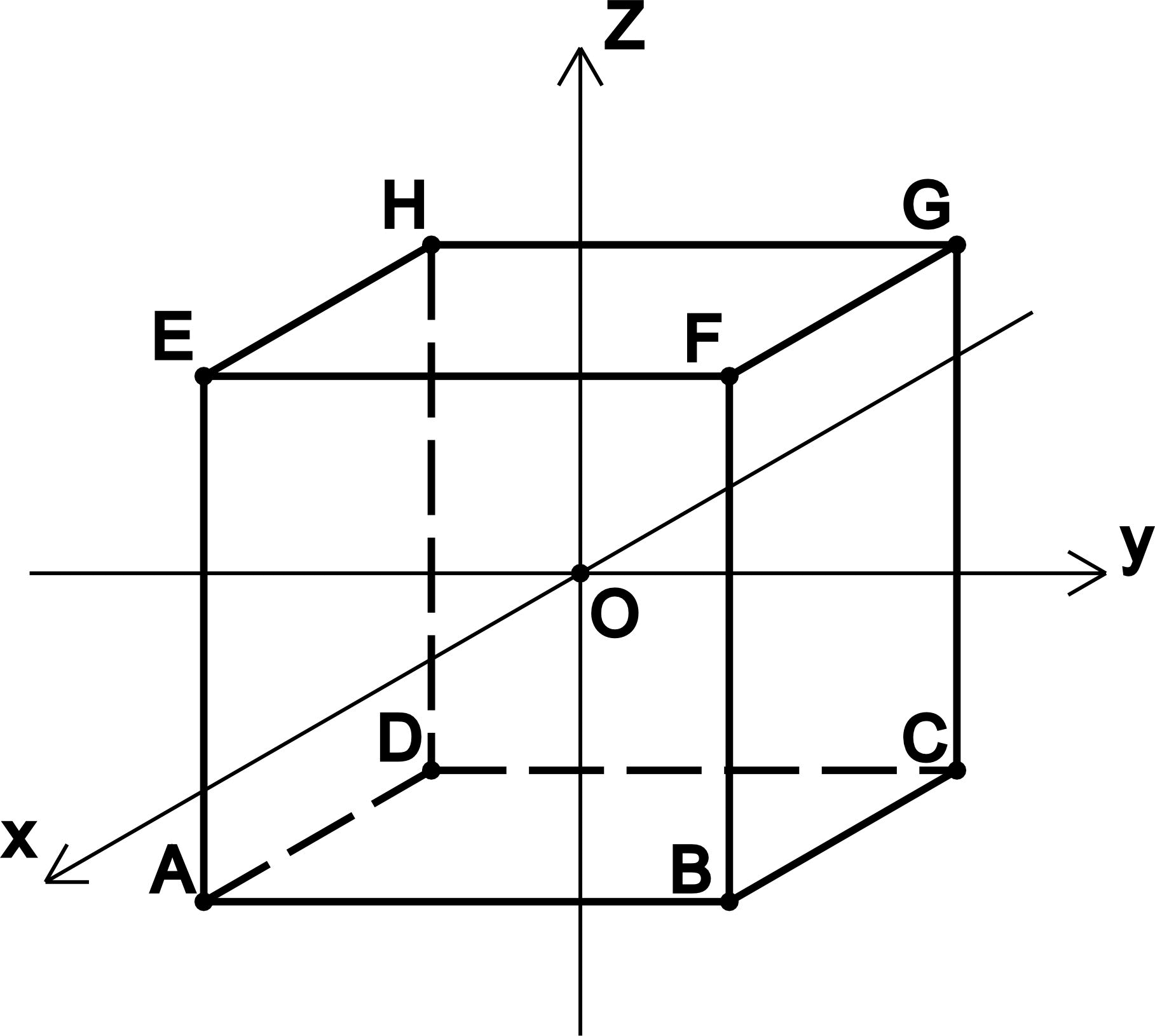
2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что рёбра куба параллельны осям координат:

$$\begin{gathered} A(a, -a, -a), B(a, a, -a), C(-a, a, -a), D(-a, -a, -a), \\ E(a, -a, a), F(a, a, a), G(-a, a, a), H(-a, -a, a). \end{gathered}$$

Единичный куб

Единичный куб  - куб, длина рёбер которого равна единице.

Пересечение единичного куба  плоскостью

1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Такая плоскость делит куб на два равных прямоугольных параллелипипеда.

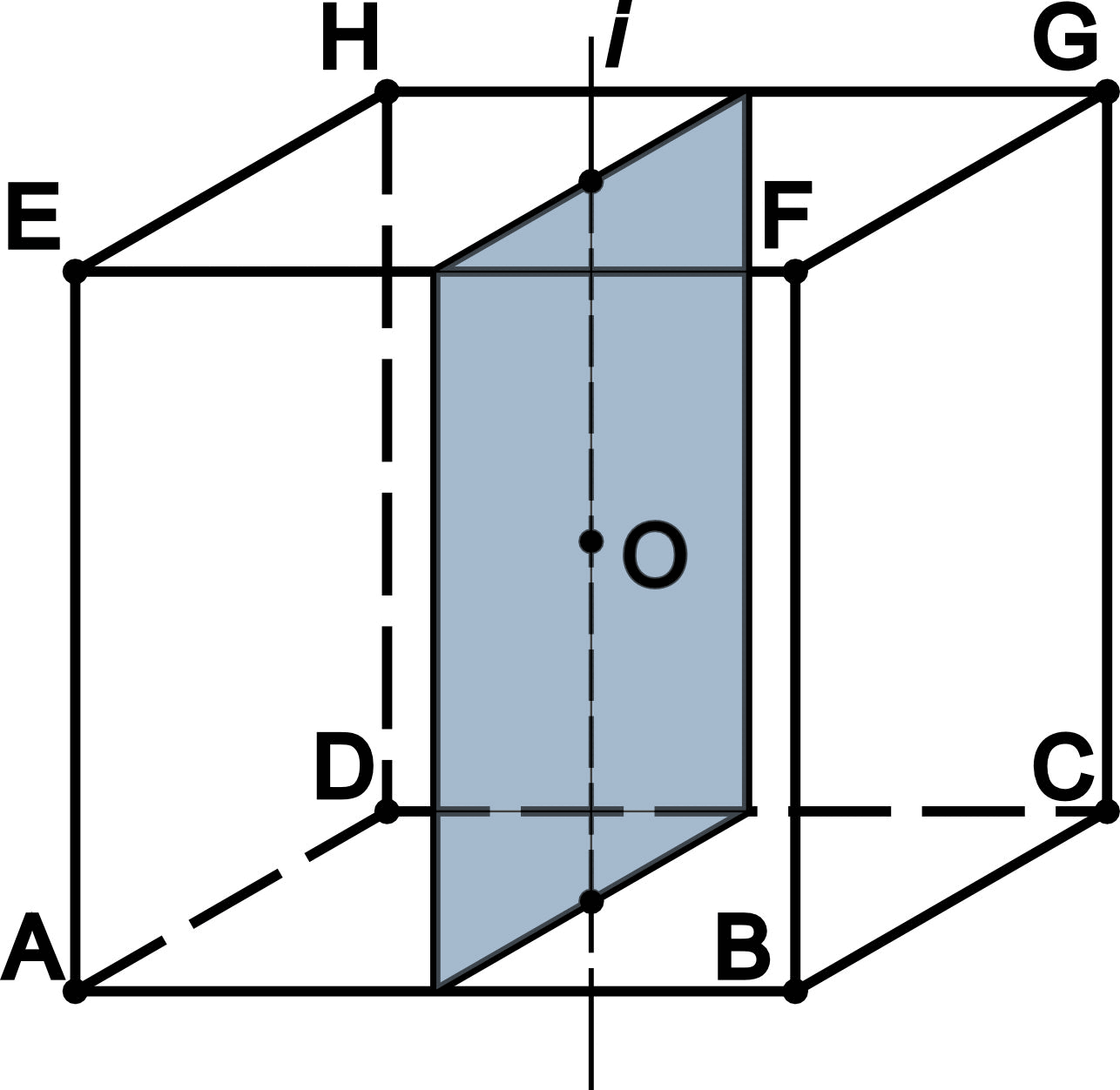
2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами $a и a\sqrt{2}$ и площадью $a^2\sqrt{2}$. Такаяя плоскость делит куб на две равные призмы.

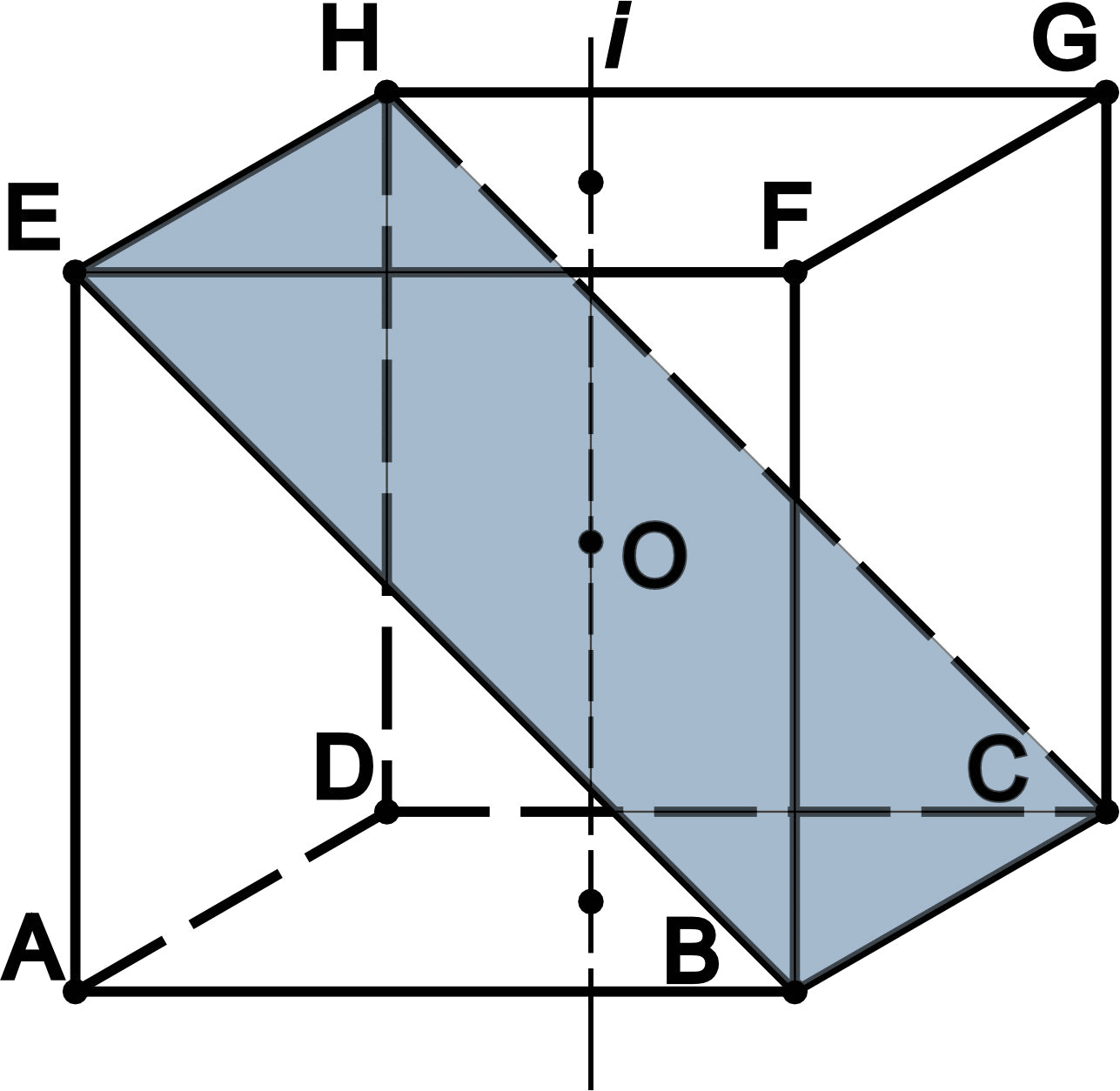
3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной $\frac{a\sqrt{2}}{2}$ и площадью $\frac{a^{2}3\sqrt{3}}{4}$. У куба одна из диагоналей (например FC) каждой грани, что пересекаются, перпендикулярна стороне такого шестиугольника.

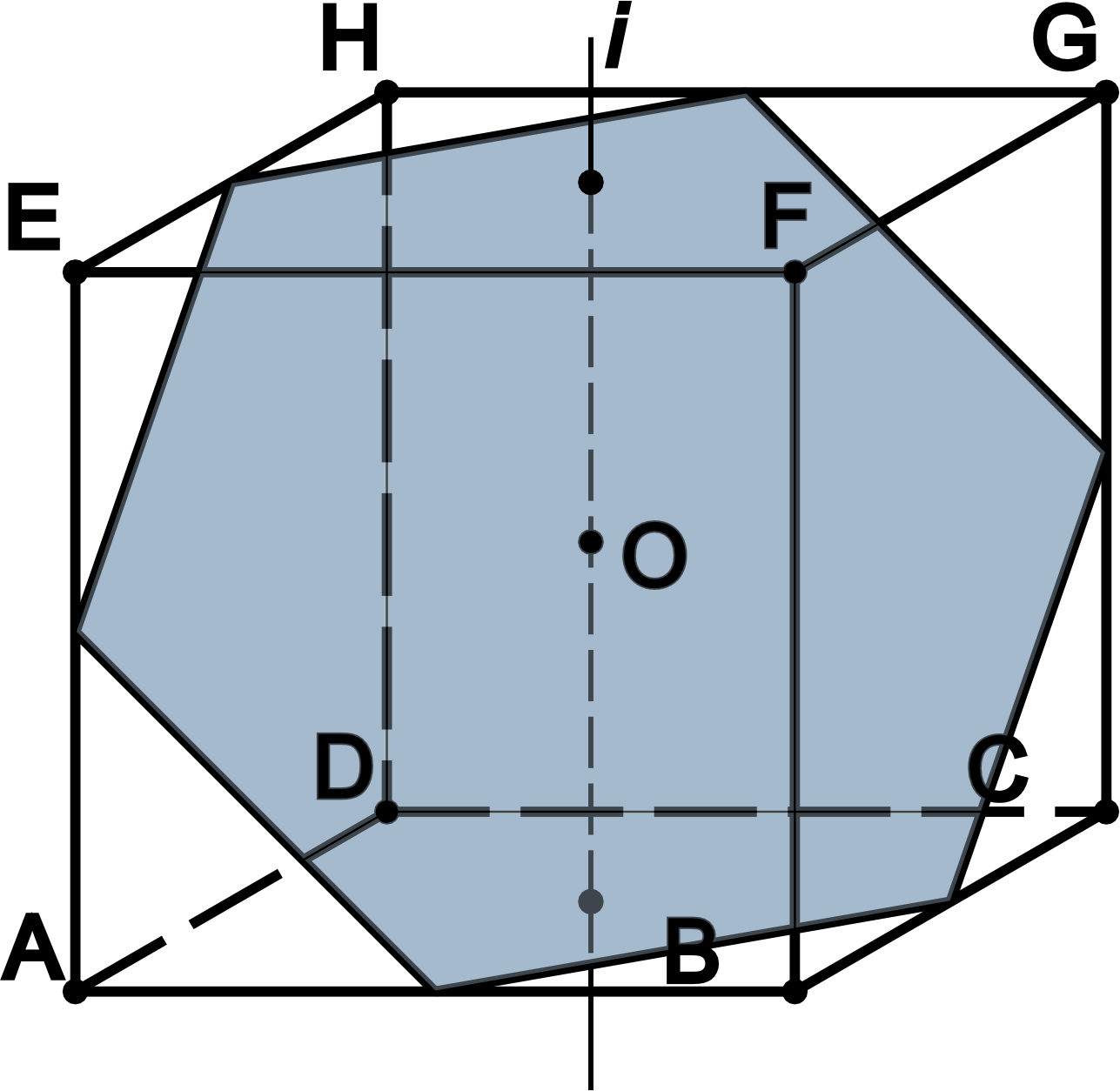
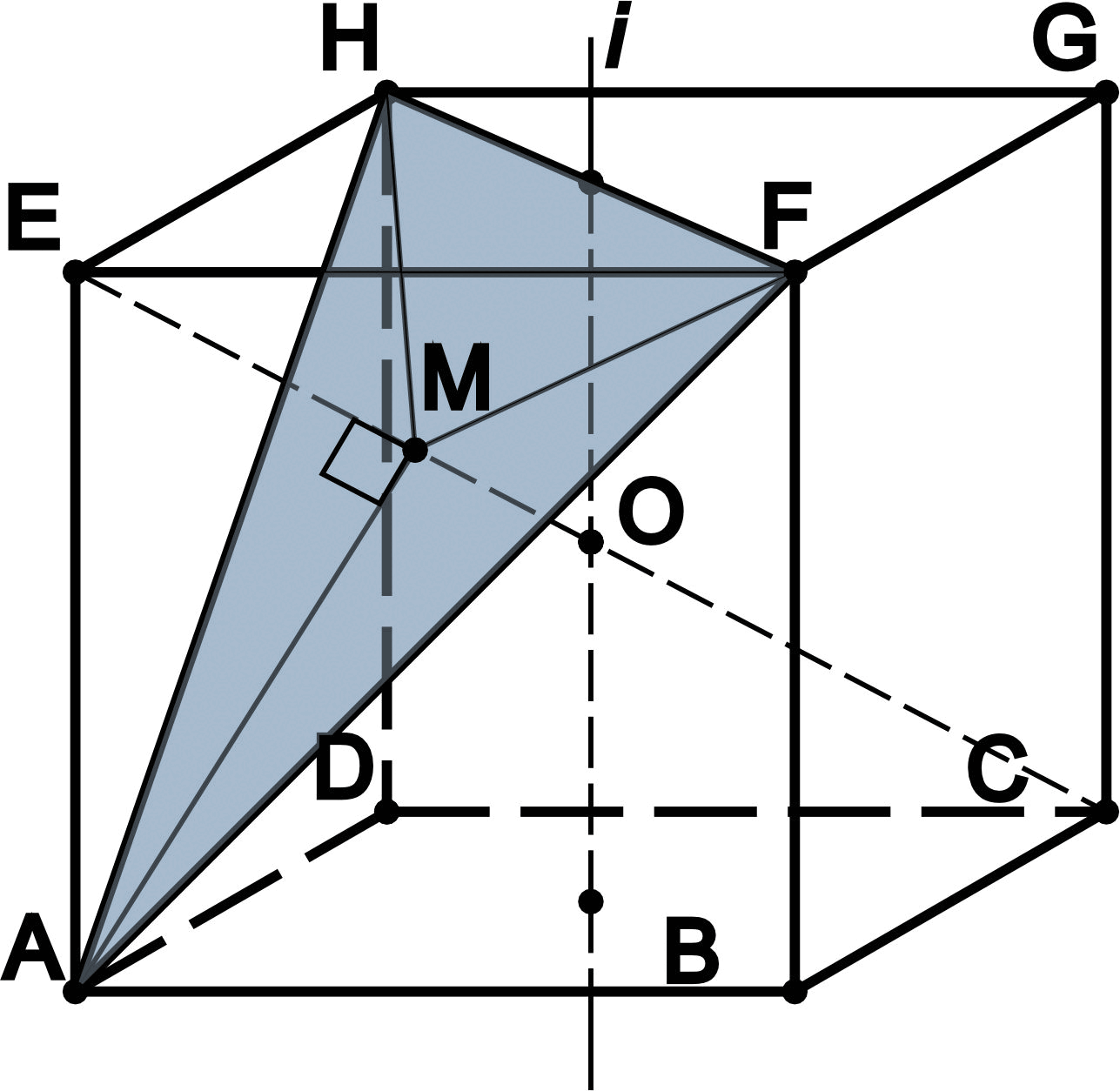
4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной $a\sqrt{2}$ и площадью сечения $\frac{a^2\sqrt{3}}{2}$. В результате сечения куб делится на большую часть объёмом $\frac{5a^3}{6}$ и меньшую объёмом $\frac{a^3}{6}$. Одна из диагоналей куба (EC) перпендикулярна плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении $MC:EM = 2:1$.