Окружность Определения и формулы
Содержание
- Определение окружности
- Определение круга
- Радиус и диаметр окружности
- Основные свойства окружности
- Формулы длины окружности и площади круга
- Уравнение окружности
- Касательная окружности и её свойства
- Секущая окружности и её свойства
- Хорда окружности и её свойства
- Центральный и вписанный угол и их свойства
- Дуга, её длина и градусная мера
- Сектор и его площадь
- Сегмент и его площадь
- Концентрические окружности и кольцо
Определение окружности
Окружность - это замкнутая плоская кривая, все точки которой равноудалены от заданной точки О на той же плоскости, называемой центром окружности. Существует несколько особых типов окружностей: единичная и нулевая.
Нулевая окружность является точкой и далее не рассматривается.
Определение круга
Круг - часть плоскости, лежащая внутри окружности. Другими словами, круг - это совокупность точек, лежащих на одной плоскости с окружностью и удаленных от её центра на расстояние меньшее либо равное радиусу окружности.
Если точки находятся на расстоянии , то такой круг называется открытым. Если же выполняется неравнество , то круг называется замкнутым. Хотя понятия окружности и круга отличаются, они обладают одинаковыми элементами (центр, диаметр и радиус).
Если точки находятся на расстоянии , то такой круг называется открытым. Если же выполняется неравнество , то круг называется замкнутым. Хотя понятия окружности и круга отличаются, они обладают одинаковыми элементами (центр, диаметр и радиус).
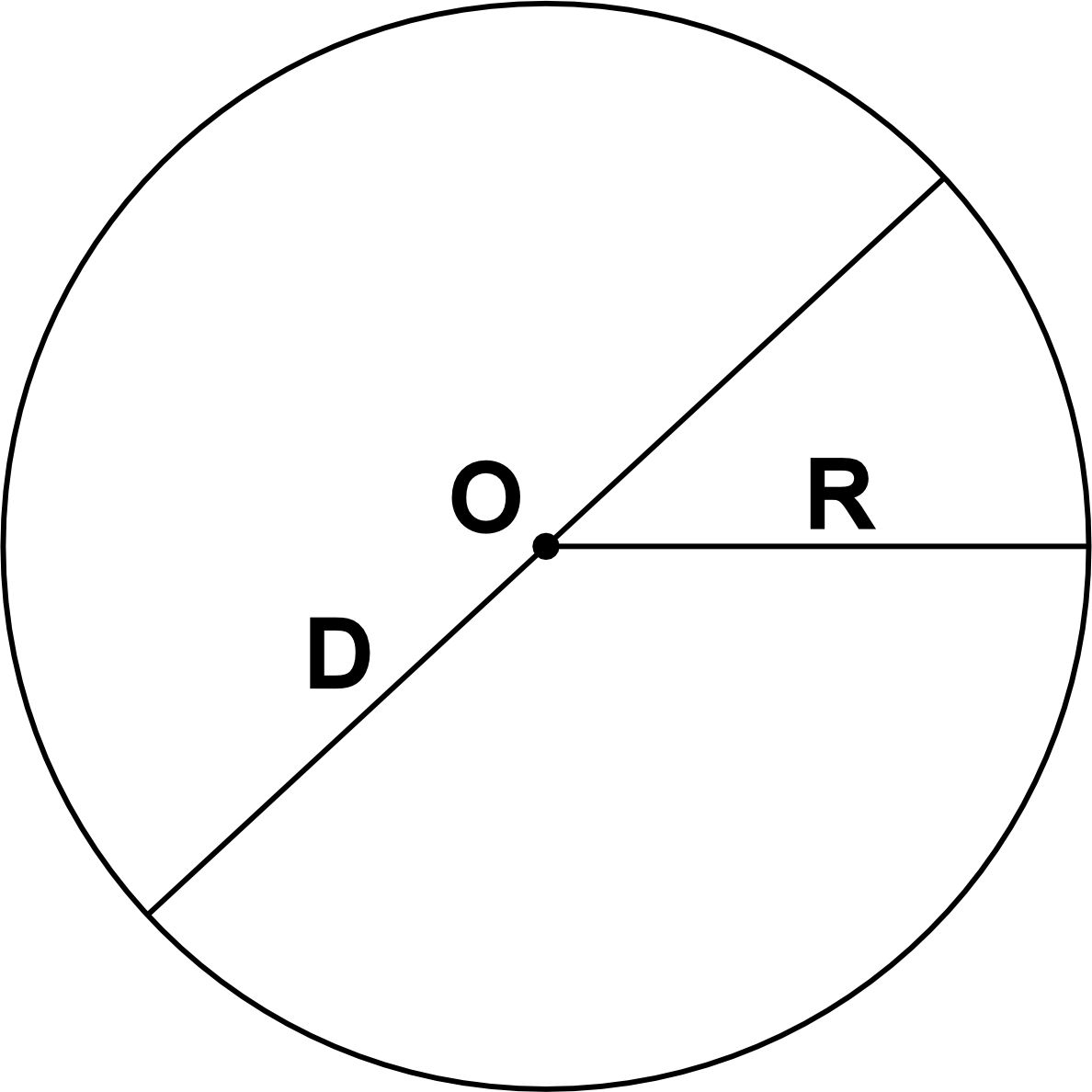
Радиус и диаметр окружности
Радиус окружности, R - отрезок, соединяющий центр окружности с любой другой её точкой. Также радиусом называют длину такого отрезка. Радиус является половиной диаметра, D.Приведём основные формулы расчёта радиуса окружности:
- Через длину окружности:
- Через площадь кргуа:
- Через диаметр:
- Через диагональ вписанного прямоугольника. Вписанным называется прямоугольник, касающийся окружности всеми своими вершинами.
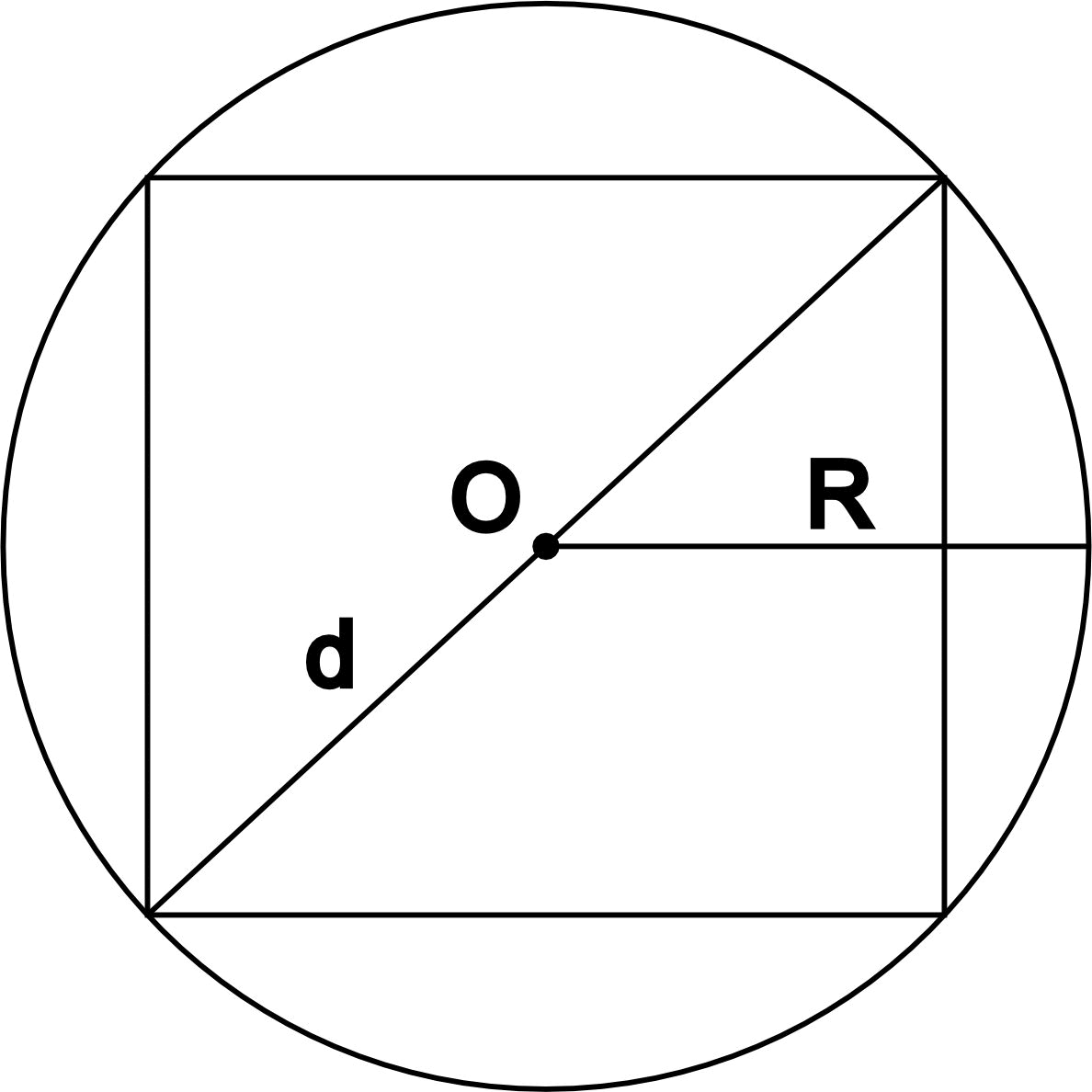
- Через сторону описанного квадрата. Описанным называется квадрат, который касается окружности всеми своими сторонами.
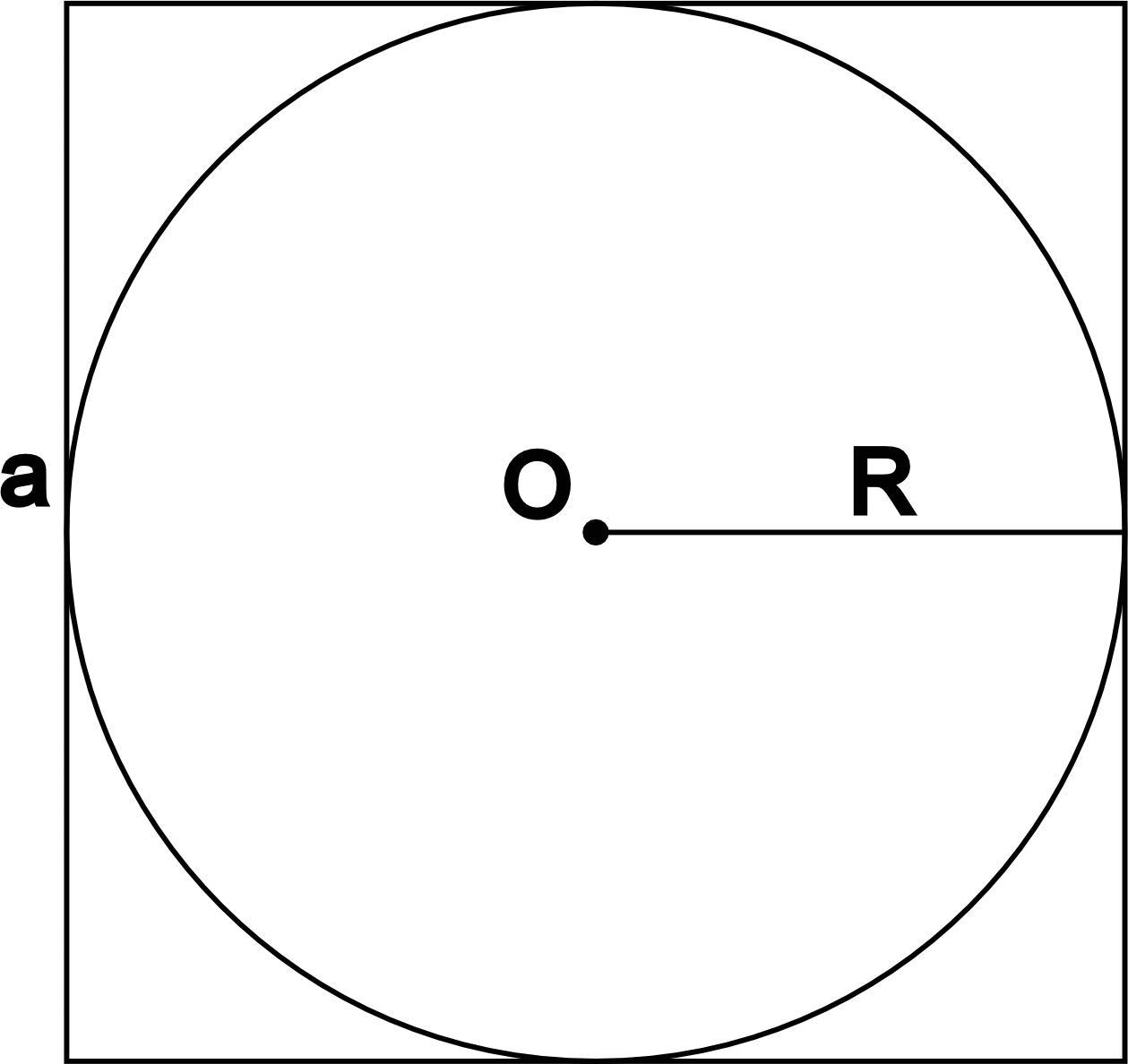
- Через размеры вписанного треугольника.
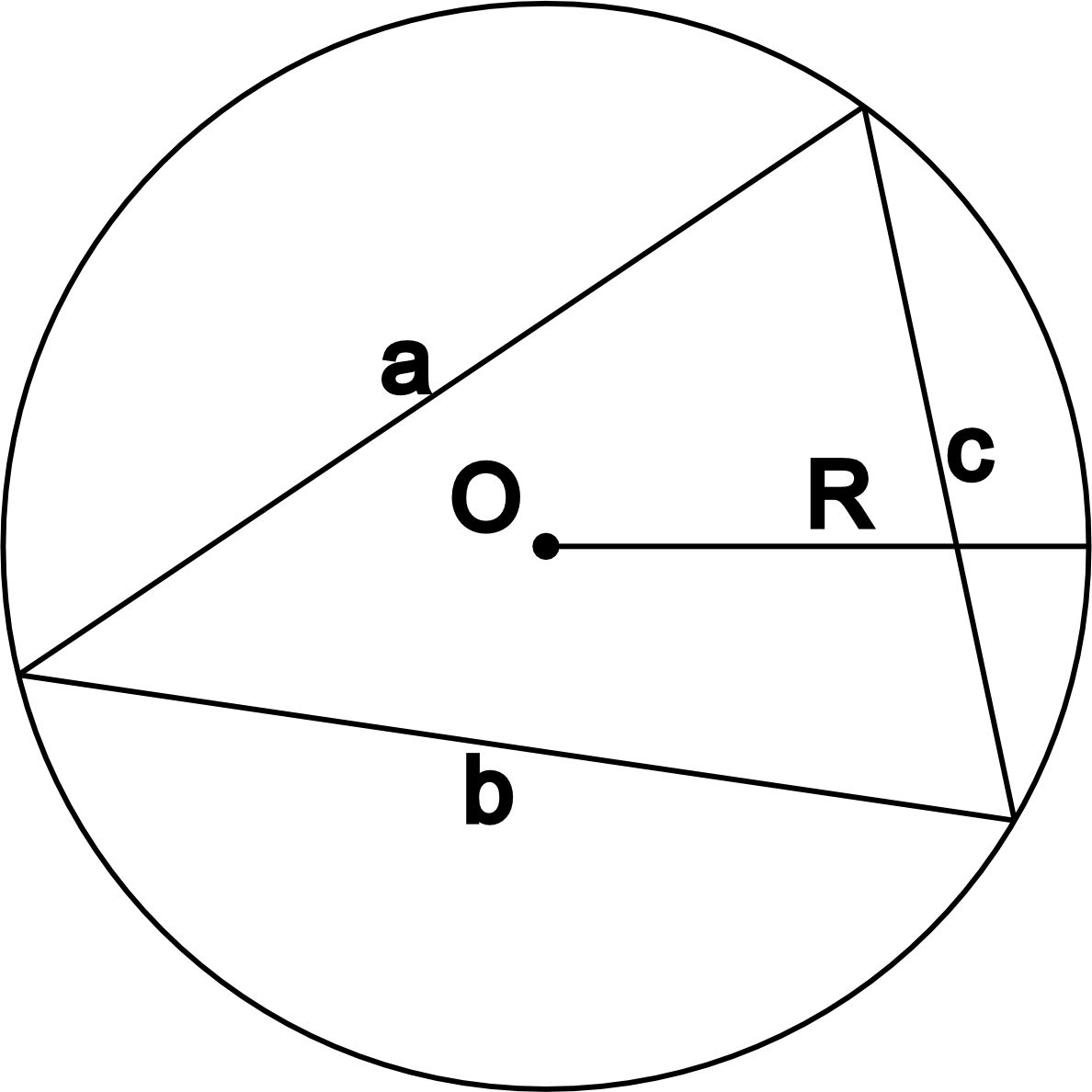
- Если треугольник является прямоугольным:
- Если треугольник является равносторонним:
- Если треугольник произвольный:
- Через размеры описанного треугольника.
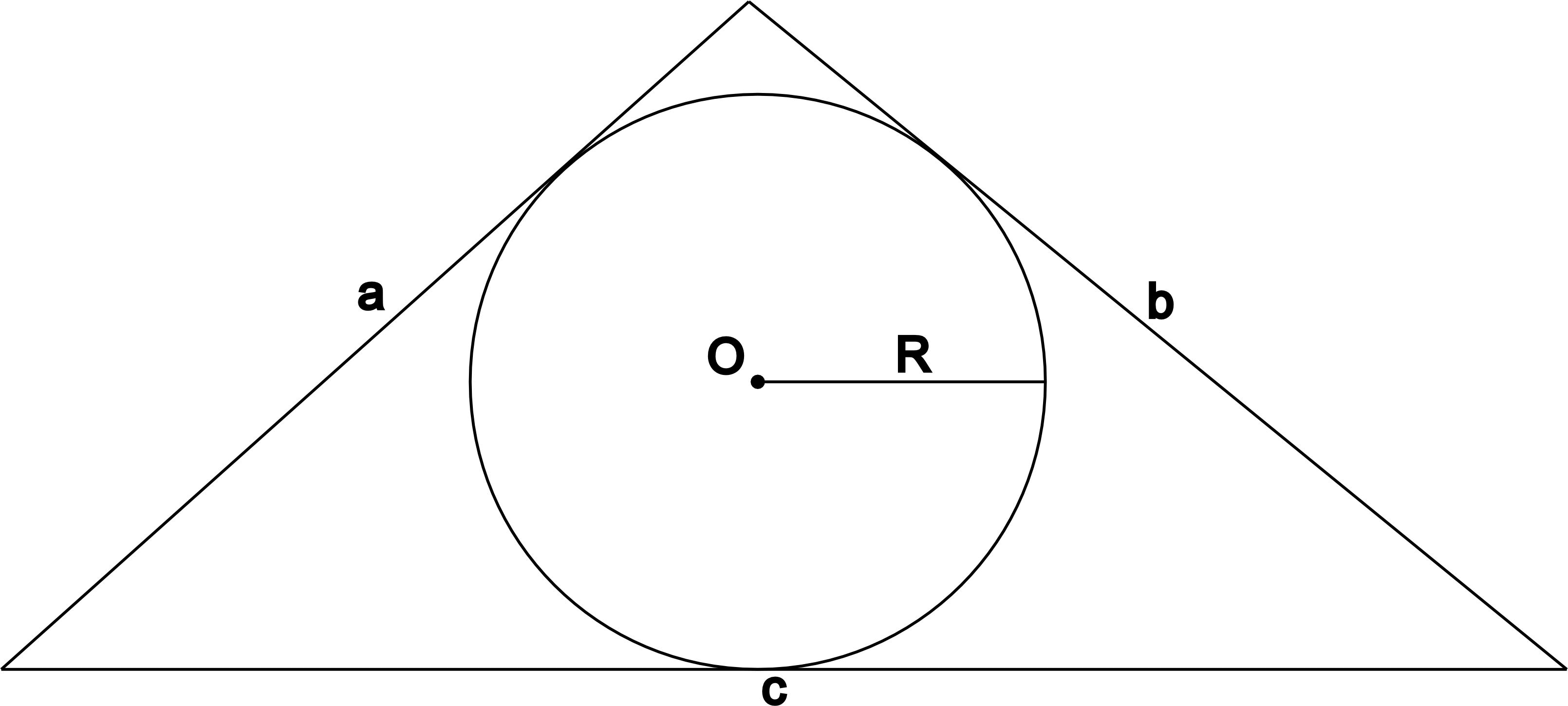
где p - полупериметр описанного треугольника, а S - его площадь. Полупериметр рассчитывается следующим образом:
где a, b и с - стороны треугольника.Диаметр окружности, D - отрезок, соединяющий две точки окружности и проходящий через её центр. Также диаметром назаывают длину такого отрезка. Диаметр является наибольшей из возможных хорд окружности.
Основная формула, которую необходимо знать для расчёта диаметра:
Остальные формулы можно получить, исходя из формул расчёта радиуса окружности.
Основные свойства окружности
- Через три точки, не лежащие на одной прямой, можно провести окружность и при том только одну.
- При условии сохранения длины среди кривых окружность ограничевает наибольшую площадь.
- Если две окружности касаются друг друга в одной точке, то эта точка лежит на прямой, проходящей через центр этих окружностей.
- Кратчайшее расстояние от центра окржности до хорды или секущей всегда меньше радиуса данной окружности.
- Градусная мекра окружности составляет 360 градусов.
Формулы длины окружности и площади круга
Длина окружности, L - это длина кривой, ограничивающей круг.Формула длины окружности: Площадь круга, S - пространство, ограниченное окружностью.
Формула площади круга:
Уравнение окружности
Уравнение окружности - выражение, которое описывает окружность на координатной плоскости. Оно имеет несколько видов:- В случае. если центр окружности находится в точке с координатами (0;0), то есть начале координат:
- В случае если центр окружности находится в точке с координатами (x0;y0):
- Параметрическое уравнение. Параметрическим называют уравнение, в котором величина выражается через некоторый варируемый в определённой области параметр.
Касательная окружности и её свойства
Касательная окружности - это прямая, которая касается окружности только в одной точке.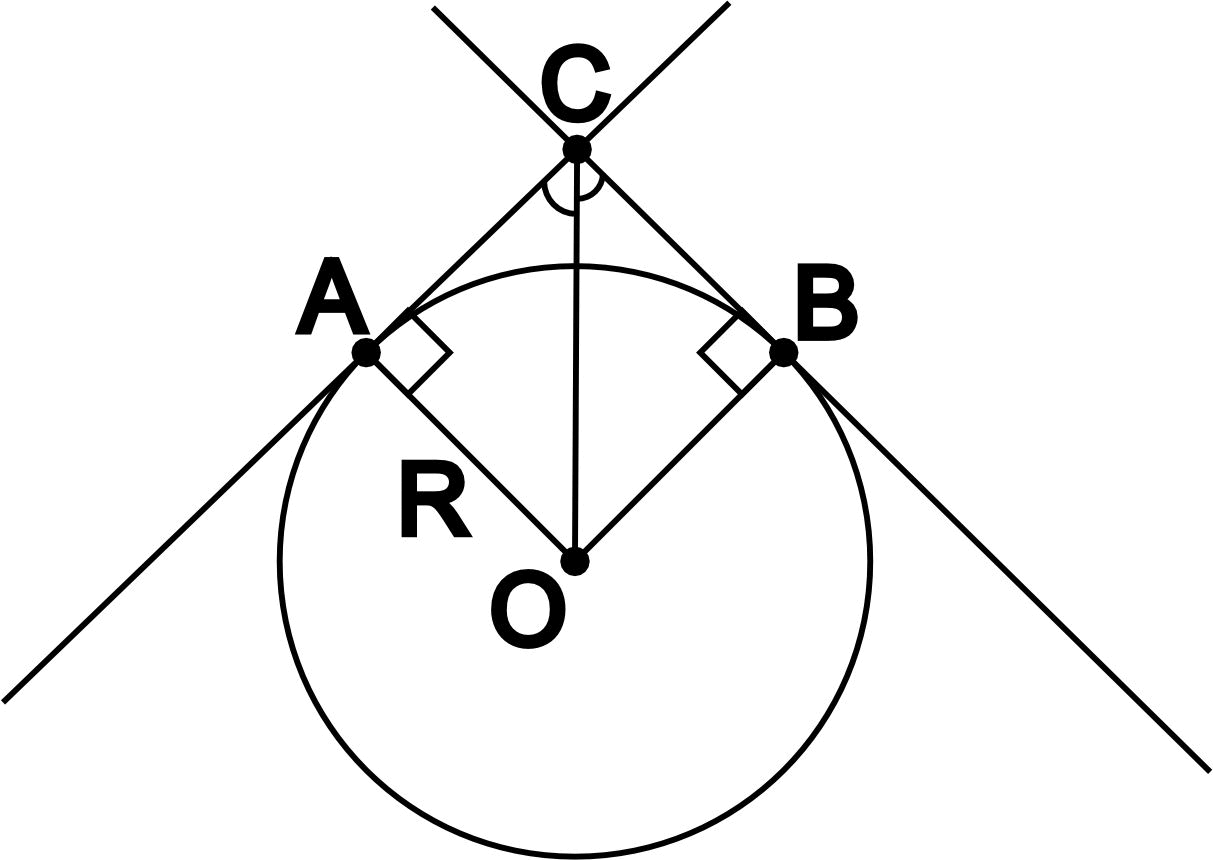
- Касательные всегда перпендикулярны радиусу, проведенному к точке их соприкосновения с окружностью.
- Кратчайшим расстоянием от центра окружности до точки её соприкосновения касательной с данной окружностью является её радиус.
- Если две касательные одной окружности не параллельны, то расстояния от точек их касания с окружностью до точки их пересечения равны.
Секущая окружности и её свойства
Секущая окружности - прямая, пересекающая окружность в двух разных точках.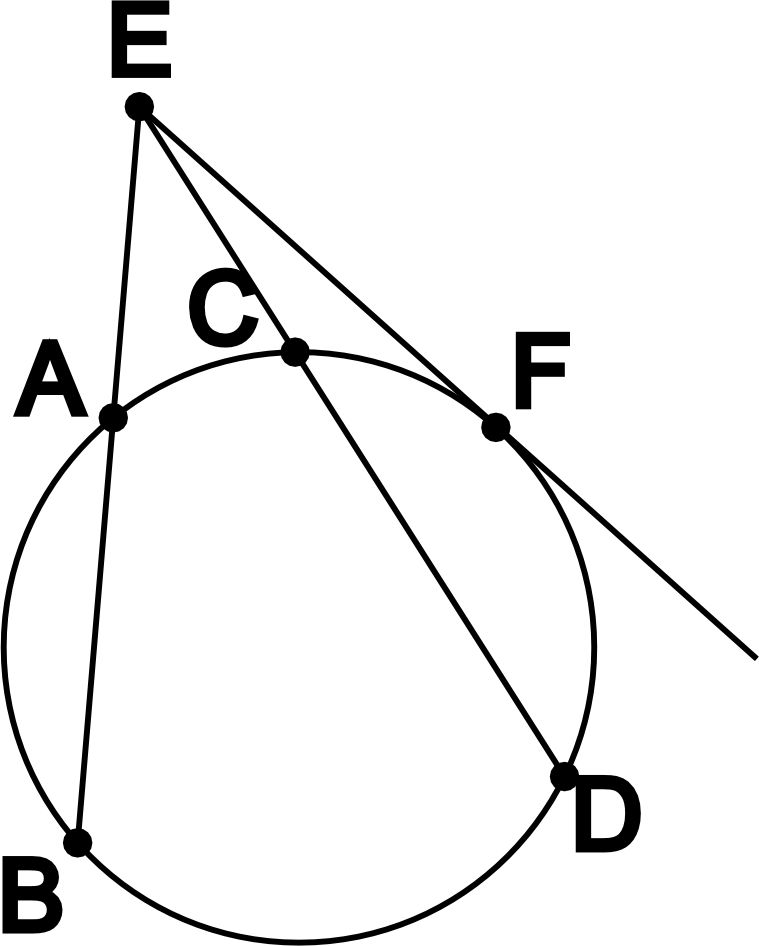
- Если две секущие исходят из одной точки вне окружности, то произведения длин отрезков от этой точки до точек пересечения секущих с окружностью будут равны.
- Если секущая и касательная исходят из одной точки вне окружности, то произведение длин отрезков от этой точки до точек пересечения секущей с окружностью будет равно квадрату длины отрезка от исходной точки до точки касания касательной с окружностью.
- Если провести отрезки от точек пересечения секущей с окружностью до точки касания её касательной, то образуются два подобных треугольника.
- Если провести отрезок между точками первого пересечения окружности двумя секущими и отрезок между точками второго пересечения окружности этими же секущими, то образуются два подобных треугольника.
- Кратчайшее растояние от центра окружности до секущей всегда меньше радиуса этой окружности.
Хорда окружности и её свойства
Хорда окружности - отрезок, соедниняющий две точки окружности. Наибольшей возможной хордой окружности является её диаметр.
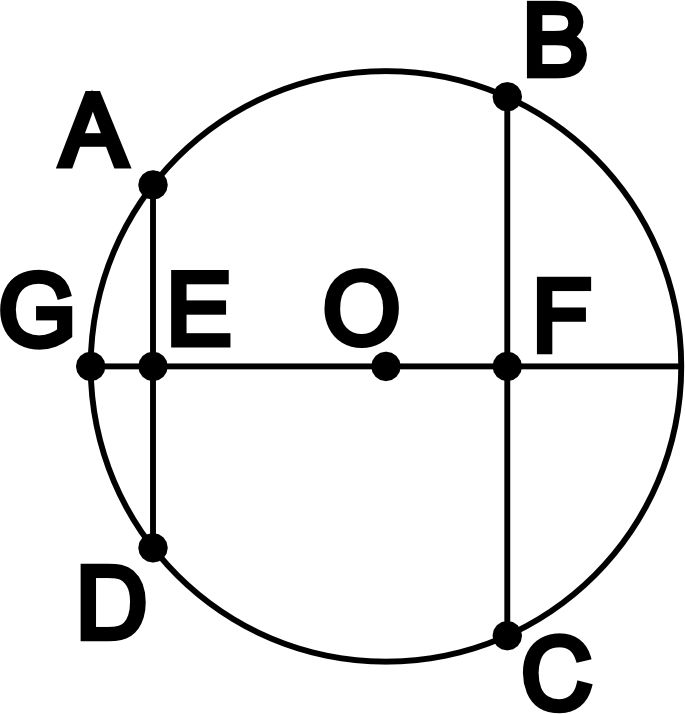
Основные свойства хорды окружности:
- Если две хорды равны, то кратчайшие расстояния от них до центра окружности одинаковы. И наоборот, если хорды находятся на одинаковом расстоянии от центра окружности, то они равны.
Также можно утверждать, что расстояние от центра окружности тем больше, чем меньше длина хорды. И наоборот, чем больше хорда, тем меньше расстояние от неё до центра окружности.
- Если расстояние от центра окружности до хорды равно нулю, то такая хорда является диаметром. Если же это расстояние равно радиусу окружности, то такая хорда вырождается в точку.
- Если диаметр перпендикулярен хорде, не являющейся диаметром, то он он делит хорду точкой пересечения пополам. Также точкой пересечения с диаметром делится пополам дуга, стягиваемая данной хордой.
- Равные хорды стягивают равные дуги.
- Если две хорды параллельны, то дуги между ними будут равны.
- Если две хорды пересекаются в некой точке, то произведения длин полученных отрезков хорд будут равны.
- Чем больше хорда, тем большую дугу она стягивает.
- Через центральный угол и радиус:
- Через вписанный угол и радиус:
Центральный и вписанный угол и их свойства
Центральный угол окружности - угол, вершина которого находится в центре окружности, а стороны пересекают окружность в двух точках, образуя между ними дугу, то есть опираются на неё.
Вписанный угол окружности - угол, вершина которого находится на окружности, а стороны пересекают окружность в двух точках, образуя между ними дугу, то есть опираются на неё.
Вписанный угол окружности - угол, вершина которого находится на окружности, а стороны пересекают окружность в двух точках, образуя между ними дугу, то есть опираются на неё.
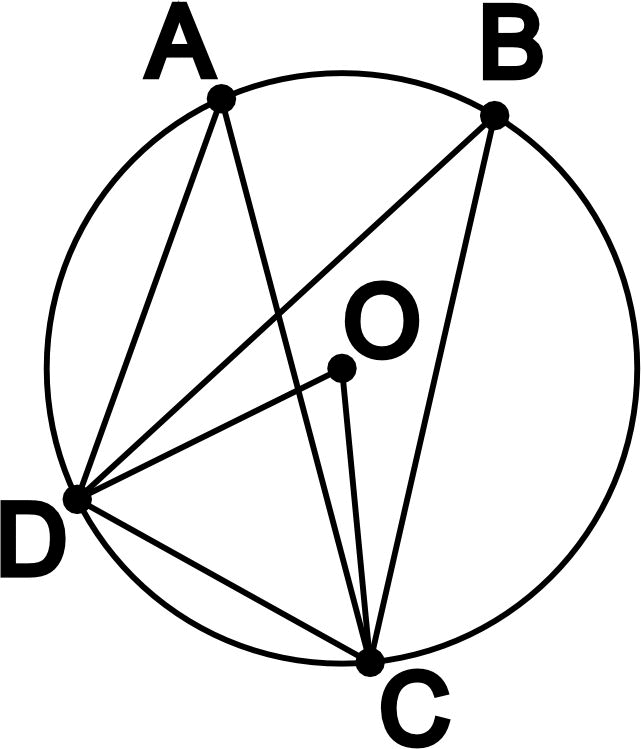
Основные свойства углов окружности:
- Вписанные углы, опирающиеся на одну дугу или хорду, равны.
- Вписанный угол, опирающийся на диаметр, является прямым, то есть равным 90 градусам.
- Если центральный и вписанный угол опираются на одну и ту же дугу или хорду, то такой вписанный угол равен половине такого центрального угла.
- Если два вписанных угла опираются на одну и ту же хорду и находятся по разные её стороны, то их сумма равна 180 градусам.
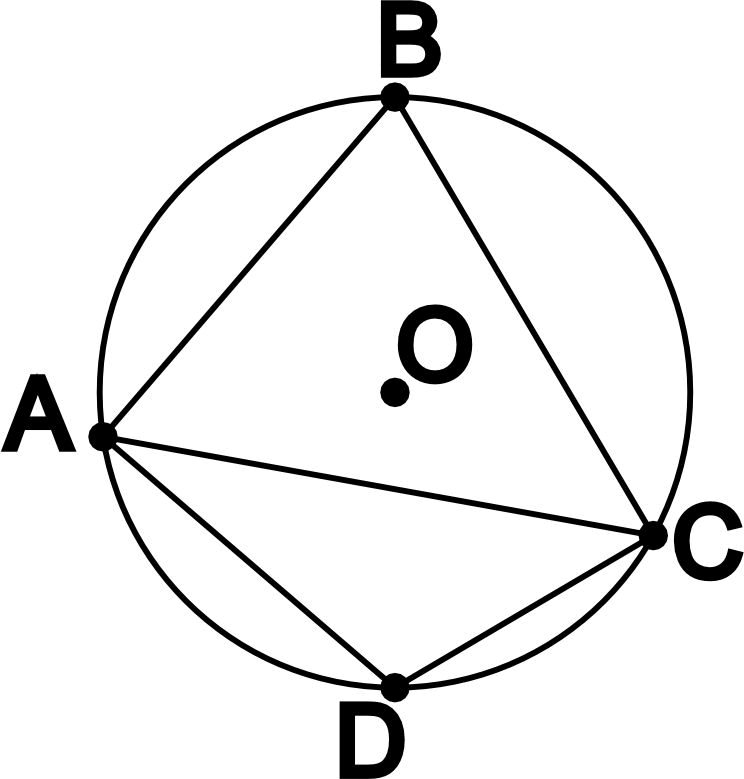
- Центральный угол равен градусной мере дуги, на которую он опирается.
Дуга, её длина и градусная мера
Дуга окружности - это одна из двух частей окружности, на которые её разбивают две лежащие на ней же точки. Любые две точкии на окружности разделяют её на две части. Обе эти части являются дугами. Отрезок, соединяющий концы дуги, является хордой и говорят, что хорда "стягивает" дугу.
Градусная мера дуги - угол между двумя радиусами, ограничивающими данную дугу.
Если точки, ограничивающие дугу, лежат на диаметре окружности, то такие точки определяют две равные дуги, называемые полуокружностями, а угол называется развёрнутым. В ином случае формируются меньшая и большая дуга, называемые дополнительными.
Часть плоскости, ограниченная полуокружностью и диаметром, называется полукругом.
Длина дуги, LD - расстояние по кривой линии между точками, ограничивающими данную дугу. Если центральный угол выражен в гадусах, она рассчитывается следующим образом:
Градусная мера дуги - угол между двумя радиусами, ограничивающими данную дугу.
Если точки, ограничивающие дугу, лежат на диаметре окружности, то такие точки определяют две равные дуги, называемые полуокружностями, а угол называется развёрнутым. В ином случае формируются меньшая и большая дуга, называемые дополнительными.
Часть плоскости, ограниченная полуокружностью и диаметром, называется полукругом.
Длина дуги, LD - расстояние по кривой линии между точками, ограничивающими данную дугу. Если центральный угол выражен в гадусах, она рассчитывается следующим образом:
где Q - центральный угол для данной дуги.
Если угол выражен в радианах, то формула приобретает вид:
Сектор и его площадь
Сектор - часть круга, ограниченная двумя радиусами данного круга и дугой между ними.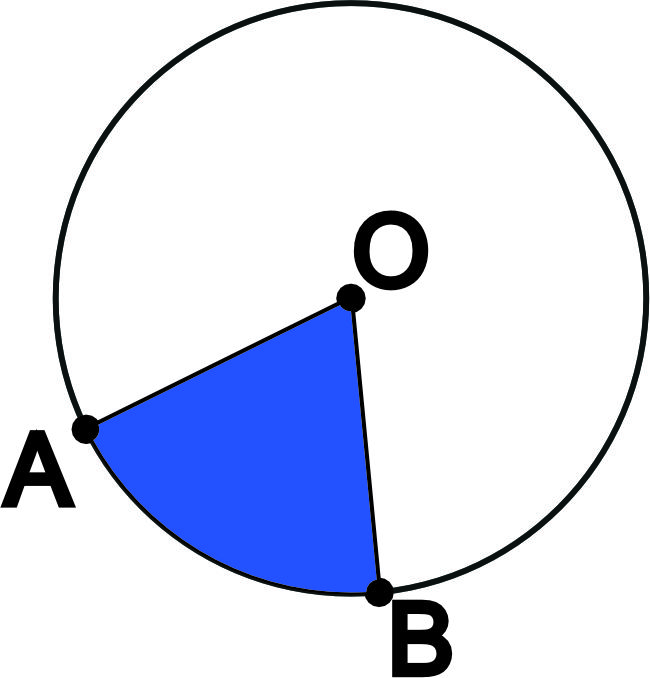
Сегмент и его площадь
Сегмент - это часть круга, ограниченная хордой и дугой, которую она стягивает.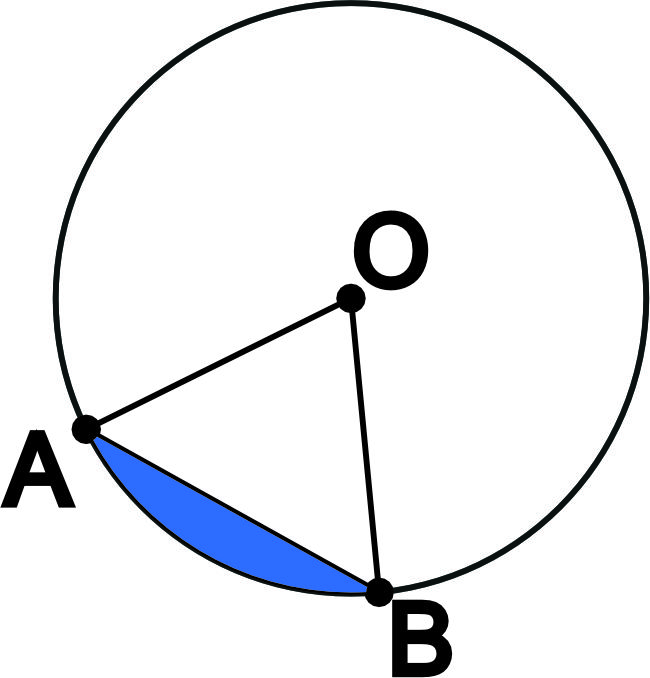
Концентрические окружности и кольцо
Концетрические окружности на плоскости - окружности с различными радиусами и общим центром. В трёхмерном пространстве концентрические окружности необязательно должны иметь различные радиусы. Концентрические окружности не имеют общих точек и точки одной окружности лежат в плоскости, ограниченной другой окружностью.