$Калькулятор дробей$

Калькулятор дробей

Рассмотрим пример решения дробей 1/2 + 1/2 = 1

Вид дроби: Простые Смешанные

Решение:

Введено

1. Сложение дробей

1+1

Ответ

Детальное объяснение решения:

1.Сложение дробей с общими знаменателями

1+1

Онлайн калькулятор дробей

Калькулятор для сложения, вычитания, умножения и деления дробей. Калькулятор может выполнять операции с двумя дробями, которые могут быть смешанными (то есть с целой частью) или простыми (без целой части). Дроби могут быть правильными или не правильными (где числитель больше знаменателя). Для ввода десятичной дроби используйте поле для целой части, а дробную часть оставьте пустой. Для ввода отрицательной дроби используйте знак "-" минус в целой части или в числителе.

Возможности калькулятора дробей:

Сложение дробей: Сложение дробей с одинаковыми знаменателями сводится калькулятором к сложению их числителей. Если знаменатели не равны то калькулятор приведет дроби к общему знаменателю.
Вычитание дробей: Вычитание дробей с равными знаменателями сводится к вычитанию их числителей.
Умножение дробей: Если дроби не имеют целой части то умножение дробей сводится калькулятором к умножению их числителей и отдельно умножению знаменателей. Иначе калькулятор сначала приведет дроби к простому виду, то есть без целой части.
Деление дробей: Деление заменяется калькулятором на умножение и достигается "переворотом" одной из дробей. То есть у одной из дробей числитель и знаменатель меняются местами и вместо деления дробей калькулятор выполняет их умножение.
Приведение к общему знаменателю: Когда требуется сложить или вычесть дроби с разными знаменателями калькулятор дробей находит наименьший общий знаменатель и вычисляет домножитель каждой из дробей. Далее производит умножение на домножитель и тем самым приводит дроби к одному общему знаменателю.
Перевод из смешанного вида в простой: При умножении или делении смешанных дробей требуется привести их к простому виду то есть без целой части. Приведение заключается в умножении целой части на знаменатель и записи результата в числитель.
Упрощение дробей: Калькулятор всегда упрошает дробь если это возможно. Упрощение может заключаться в сокращении дроби или переводом ее из дробного вида к целому числу.
Нахождение НОЗ: Калькулятор находит наибольший общий знаменатель если это требуется в операциях умножения или упрощения дробей.
Интуитивно понятный интерфейс: Калькулятор имеет простые поля для ввода дробных чисел что соответствует общепринятым правилам при работе с дробями.
Решение шаг за шагом: Калькулятор дробей разделяет процесс вычисления на несколько логических шагов. Каждый из которых имеет подробное описание с выводом всех промежуточных действий.

Наш калькулятор дробей будет полезен всем кому требуется решить дробные выражения и получить подробное решение с ответом.

Что такое дробь

Дробь - это одно число у которого есть числитель и знаменатель.
Знаменатель означает на сколько равных частей поделено целое, а числитель - сколько таких частей взято.

Обыкновенная Дробь записывается "в два этажа". В верхний этаж записывается числитель, а в нижний знаменатель.

Пример обыкновенной (простой) дроби:
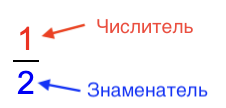
Дробь с числителем и знаменателем

Если у дроби есть целая часть то такая дробь называется смешанной.

Пример смешанной дроби:
$3 \frac{1}{2}$
где 3 - целая часть, 1 - числитель, 2 - знаменатель.

Целая часть записывается перед дробью и должна располагаться посередине между числителем и знаменателем.

Целая часть всегда подразумевает следующее сотношение:
$3 \frac{1}{2} = 3 + \frac{1}{2}$

Это означает что любая смешанная дробь подразумевает сложение целого числа с обыкновенной дробью.

Как решать дроби самостоятельно

Чтобы научиться решать дроби самостоятельно необходимо следовать общепринятым правилам операций с дробями. Всего может быть четыре основных действия - это сложение, вычитание и умножение, деление дробей. А также три дополнительные - сокрашение, выделение целой части, перевод из смешанного вида в простой. Выучив данные семь правил Вы сможете самостоятельно выполнять любые операции с дробями.

Сложение дробей

Сложение дробей выполняется в 6 шагов:

Определение типа дробей: Если дроби смешанные то сложение дробей рациональней выполнить раздельно - сначала для целых частей, затем для дробных. Тоесть сначала складываем целые части между собой как обычные числа, затем приступаем к сложению дробных частей.
Проверка знаменателей: Если знаменатели дробей равны то данный шаг можно пропустить иначе необходимо привести дроби к одному общему знаменателю. Сначала требуется его найти. Для этого проще всего - это перемножить знаменатели, но в некоторых случаях знаменатель одной из дробей уже может являться общим. Или еще рациональней найти НОЗ - наименьший общий знаменатель по алгоритму поиска НОД двух чисел. И в последующем вычислить домножитель каждой из дробей.
Умножение числителей на домножители: Данный шаг выполняется только если были вычислены домножители в предыдущем шаге и они не равны единице. Заключается в умножении числителя и знамнателя на домножитель.
Сложение числителей: Просто сложите числители как целые числа и запишите полученный числитель оставив один общий знаменатель.
Проверьте, можно ли сократить дробь: Если числитель и знаменатель можно разделить без остатка на какое-то целое число то значит дробь сокращаема. Определить это число можно отыскав НОД числителя и знаменателя.
Выделение целой части: Если в получившимся ответе числитель больше знаменателя то такую дробь можно перевести в смешанный вид выделением целой части. Для этого достаточно разделить числитель на знаменатель с учетом остатка от деления. Целым от деления является целым дроби, а остаток от деления - новым числителем. Знаменатель при этом не меняется.

Пример:
$\frac{1}{4} + \frac{2}{4} = \frac{1 + 2}{4} = \frac{3}{4}$

Вычитание дробей

Вычитание дробей выполняется по той же инструкции что и сложение дробей, только вместо операции сложения числителей выполнятеся вычитание числителей. Если результатом вычитания числителей становится ноль, то и результатом вычитания дробей является ноль.

Пример:
$\frac{3}{5} - \frac{2}{5} = \frac{3 - 2}{5} = \frac{1}{5}$

Умножение дробей

Умножение дробей следует выполнять в такой последовательности:

Запишите дроби под одну черту: Перепишите умножение дробей в виде одной дроби в которой умножаются числители и умножются знаменатели.
Сокращение (если возможно): Проверьте, можно ли сократить числитель от одной дроби со знаменателем от другой дроби. Для этого найдите общий делитель числителя и знаменателя и разделите их на него.
Умножите числители: умножить числитель первой дроби на числитель второй дроби.
Умножьте знаменатели: умножить знаменатель первой дроби на знаменатель второй дроби.
него.
Выделение целой части: если числитель больше знаменаеля, то переведите дробь к смешанному виду.

Пример:

\frac{3}{4} \cdot \frac{4}{15} = \frac{3 \cdot 4}{4 \cdot 15}

Деление дробей

Чтобы разделить одну дробь на другую необходимо:

Перевернуть любую дробь: найти обратную дробь от любой из двух дробей. Для этого необходимо поменять числитель и знаменатель местами.
Умножение дробей: умножить полученную дробь на вторую дробь.
Сократите дробь (если возможно): проверьте, можно ли сократить полученную дробь. Для этого найдите общий делитель числителя и знаменателя и разделите их на него.
Выделение целой части: если числитель больше знаменаеля, то переведите дробь к смешанному виду.